 大きさ
大きさである。この大きさは,
である。ここで
電流が作る磁界について,右ねじの法則を見つけたのはエルステッド(Oersted 1820)であったが,これを定量的に式で表したものがビオ=サバールの法則である。
 大きさ
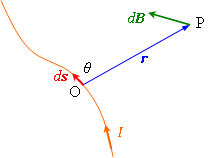
大きさ![]() の電流上の点
の電流上の点![]() にある微小な長さ
にある微小な長さ![]() の部分が
の部分が![]() で指定される点
で指定される点![]() の位置に作る磁束密度(磁界)は,
の位置に作る磁束密度(磁界)は,
![]()
である。この大きさは,
![]()
である。ここで![]() は,
は,![]() と
と ![]() のなす角である。
のなす角である。
BiotとSavartは,Laplaceからこの式の形を示唆され,これを確認する実験を行ったが,技術的に困難な実験であったので,結果はさほど正確なものではなかった。
この法則は,磁荷に対するクーロンの法則と電流に働く力を使っても導き出すことができる。
 例1 無限直線電流から距離
例1 無限直線電流から距離電流の位置に![]() 軸をとり,磁束密度を求める点
軸をとり,磁束密度を求める点![]() が
が![]() の平面上にくるよう座標系をとる。
の平面上にくるよう座標系をとる。
図より,![]() であるから,長さ
であるから,長さ![]() の微小部分が作る磁束密度は,
の微小部分が作る磁束密度は,
![]()
となる。これを,積分して,
![]()
![]()
が得られる。(磁束密度の向きは右ねじの法則で決まり,この図の場合は,画面の奥へ向かう向きである。)
※この例の結果は,アンペールの定理を使うと,ごく簡単に得られる。
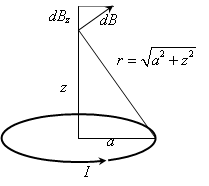 例2 円形電流の中心軸上の磁束密度
例2 円形電流の中心軸上の磁束密度円形電流![]() の中心軸上で中心から
の中心軸上で中心から![]() の距離にある点における磁束密度を考える。電流の微小部分
の距離にある点における磁束密度を考える。電流の微小部分![]() が作る磁束密度の大きさは,
が作る磁束密度の大きさは,
![]()
であるが,対称性から中心軸方向の成分
![]()
だけを積分すればよい。
![]()
![]()
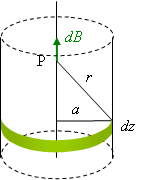 例3 無限ソレノイドの内部の磁束密度
例3 無限ソレノイドの内部の磁束密度半径![]() ,単位長さ当たりの巻き数
,単位長さ当たりの巻き数![]() のソレノイドに電流
のソレノイドに電流![]() を流したときの中心軸上の磁束密度を求める。
を流したときの中心軸上の磁束密度を求める。
図の幅![]() の部分の電流は
の部分の電流は![]() であるから,この部分が作る磁束密度は,円形電流の場合の結果を使って,
であるから,この部分が作る磁束密度は,円形電流の場合の結果を使って,
![]()
であることがわかる。これを,![]() で積分して,
で積分して,
![]()
![]()
となる。
この例の結果は,アンペールの定理を使うと,ごく簡単に得られる。さらに,中心軸上に限らず,ソレノイドの内部の磁束密度はどこでも一定であることを示すことができる。
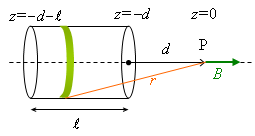 例4 有限ソレノイドの中心軸上の磁束密度
例4 有限ソレノイドの中心軸上の磁束密度前の例と同様に,半径![]() ,単位長さ当たりの巻き数
,単位長さ当たりの巻き数![]() のソレノイドに電流
のソレノイドに電流![]() を流すとする。ただし,ソレノイドの長さ
を流すとする。ただし,ソレノイドの長さ![]() は有限である。
は有限である。
ソレノイドの一端から距離![]() の位置での磁束密度は,前例と右図を参照すると,次のように計算できる。
の位置での磁束密度は,前例と右図を参照すると,次のように計算できる。
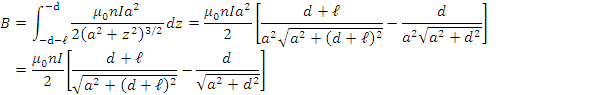
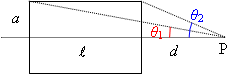 右図の角度
右図の角度![]() を使うと,
を使うと,![]() と書くこともできる。
と書くこともできる。
特に,ソレノイドの端(![]() )では,
)では,
![]() となる。
となる。
この式で![]() とすると,
とすると, ![]() となり,無限ソレノイドの内部の場合の半分になる。
となり,無限ソレノイドの内部の場合の半分になる。
問1 ソレノイドの内部(例えば,![]() )の磁束密度は,
)の磁束密度は,
![]() のとき,
例3の無限ソレノイド内部の磁束密度になることを確認せよ。
のとき,
例3の無限ソレノイド内部の磁束密度になることを確認せよ。
(ヒント) ![]() , または,
, または,![]() を使う。
を使う。
問2 全巻数![]() を一定にしたまま,
を一定にしたまま, ![]() とすると,例2の円形電流の式に帰着することを示せ。
とすると,例2の円形電流の式に帰着することを示せ。
(ヒント)![]() が小さいときは,次の近似式が使える。
が小さいときは,次の近似式が使える。
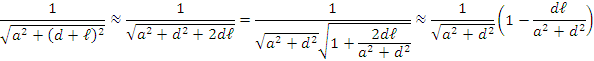
ヘルムホルツコイルは,2つの同じ円形コイルをその半径だけ離して,平行に置いたものである。
この中心付近の磁場は,ほぼ一様な磁場になり,ソレノイドよりも実験に便利であるため,さまざまな実験に使われている。
巻き数![]() ,半径
,半径![]() の円形コイルを同軸にして距離
の円形コイルを同軸にして距離![]() だけ離した置いたときの,中心部の磁束密度は,例2の円形コイルの場合の結果を用いると,
だけ離した置いたときの,中心部の磁束密度は,例2の円形コイルの場合の結果を用いると,
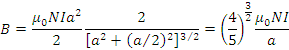
となる。これがヘルムホルツコイルによる磁束密度である。
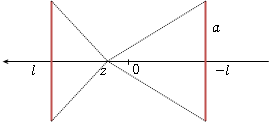
この磁場が一様なものであることを示すため,2つのコイルを![]() 離して置いたとする。(
離して置いたとする。(![]() の場合がヘルムホルツコイルである。)
の場合がヘルムホルツコイルである。)
両コイルの中心軸をz軸として,原点を両コイルの中央とするとき,まず![]() 軸上の磁束密度を求める。
軸上の磁束密度を求める。
軸上の![]() の位置での磁束密度は,
の位置での磁束密度は,
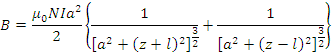
となる。
これを![]() で微分して,
で微分して,![]() での微分係数を求めると,
での微分係数を求めると,
![]() ,
, 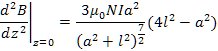 ,
, ![]()
などとなる。
ヘルムホルツコイル(![]() )のときは,2階の微分係数も0となり,
)のときは,2階の微分係数も0となり,
![]()
となり,中心軸上の中心付近は非常に一様な磁場になる。
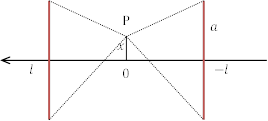
次に,![]() の位置で,中心軸から距離
の位置で,中心軸から距離![]() の点
の点![]() における磁束密度を考えよう。
における磁束密度を考えよう。
図の![]() の位置における長さdsの部分の電流が
の位置における長さdsの部分の電流が![]() の位置に作る磁束密度
の位置に作る磁束密度![]() の
の![]() 成分
成分![]() を考えればよい。
を考えればよい。
![]()
![]()
であるから,
![]()
,したがって,
![]()
となる。ここで,
![]()
である。
これより,![]() 点の磁束密度の大きさは,
点の磁束密度の大きさは,
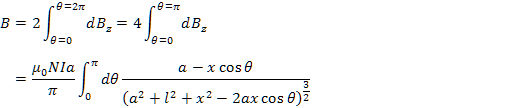
となる。
この定積分は楕円関数で書けるが,面倒なのでグラフだけを示しておく。
グラフより,ヘルムホルツコイル(![]() )は中心軸に垂直な方向にずれても,中心軸上とほとんど変わらない磁束密度を作り出すことがわかる。
)は中心軸に垂直な方向にずれても,中心軸上とほとんど変わらない磁束密度を作り出すことがわかる。
(参考) 比電荷の測定装置では,ヘルムホルツコイルが使われるが,コイルの半径15cmに対して,電子の円運動の半径は5cm程度である。そのため,磁束密度は中心での値と同じであるとして計算してもよいことがわかる。