磁荷に対するクーロンの法則

電荷と同様に磁荷 というものを考えることができ，正()の磁荷は 極，負()の磁荷は 極に対応する。電磁気学の理論的枠組みでは，電気と磁気は完全に対称的である。
しかし，現実の世界には単独の磁荷（単磁極：magnetic monopole）は見つかっていない。
なぜ単磁極が存在しない（極めて少ない？）のかを説明する理論的な枠組みも考えられている。

現実の世界の磁気は，（雑にいうと）電荷の運動つまり電流が元になっており，必ず 極と 極が対で現れる。

というわけで，磁荷そのものを扱う機会はないが，解説は電気と同じようにクーロンの法則から始めるのが見通しがよいかもしれない。
ところが，ここに厄介な問題があり，磁荷には以下の２通りの定義が使われているのである。

※以下は，必要なときに参照すればいいでしょう。

EB対応		EH対応
クーロンの法則　　　　　　　　 磁荷 と が距離 に置かれているとき，各磁荷に働く力は次式になる。
磁荷の単位は，		磁荷の単位は，（ウェーバー）
は真空の透磁率　 ここで単位 は， などと書いておく方がわかりやすい。 （ヘンリー）はコイルのインダクタンスを表す単位， （ウェーバー）は磁束を表す単位である。 対応と 対応では，磁荷の定義が 倍異なる。
磁束密度 の定義 磁荷 に働く力 によって，その点の磁束密度 を定義する。		磁界（磁場） の定義 磁荷 に働く力 によって，その点の磁界（磁場） を定義する。
これは，電荷 に働く力 により，電界（電場） を定義したことと対応している。 対応， 対応という呼び方もここに由来する。
磁界（磁場） は， で定義する。		磁束密度 は， で定義する。
もちろん， や は，いずれの定義から出発しても同じものである。 磁束密度 の単位としては， (テスラ)，， 磁界（磁場） の単位としては， （アンペア・ターン・メートル）が使われる。

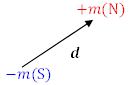
さて，磁荷を直接扱うことはまずないが，磁石のようにN極とS極が対になった磁気双極子は身近なものである。右図のように， の磁荷が距離 に置かれているとき，この磁石の強さ（磁気双極子モーメント ）は， で定義される。これは，磁荷の定義の違いを反映してしまう。

EB対応		EH対応
磁気モーメントの単位		磁気モーメントの単位
面積 のコイルに電流 が流れたときの磁気モーメント		面積 のコイルに電流 が流れたときの磁気モーメント
磁気モーメント に働くトルク		磁気モーメント に働くトルク

※教科書により，どちらを採用しているのかが異なりますので，注意が必要です。

※このように厄介な問題があるので，クーロンの法則は使わず，次に説明するローレンツ力で を定義してしまうこともできます。
しかし，この場合も磁気モーメントの定義には2通りの可能性があります。