右図のように，一様な磁束密度
が画面手前から向こう側に向いている。
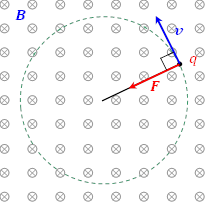
右図のように，一様な磁束密度 が画面手前から向こう側に向いている。
（注）は手前から向こうを表す記号である。 逆に，向こうから手前の向きを表すのは
を使う。
この磁場の中で正の電荷
が
速度
で動くと，
ローレンツ力
の向きは，
フレミングの左手の法則により，進行方向に垂直で左向きで，その大きさは，
である。
進行方向に垂直で一定の大きさの力を受ける物体は円運動をする。
その円運動の半径を
，
物体の質量を
とすると，
この円運動に必要な向心力
がローレンツ力で与えられているので，
が成り立つ。
これより，円運動の半径は
，
その周期は
となることがわかる。
このような磁場の中での荷電粒子の円運動をサイクロトロン運動という。
なお，図において，荷電粒子の速度
が画面に垂直な（に平行な）
成分も持っているとしてもローレンツ力は変わらない。その場合，荷電粒子は螺旋運動をすることになる。
)の測定一般に粒子の電荷 を
粒子の質量
で割った量
を比電荷（specific charge）という。
電子の電荷は
（
は電気素量）であるが，
符号は無視し，
を電子の比電荷という。
磁場中の電子のサイクロトロン運動から電子の比電荷を求めることができる。
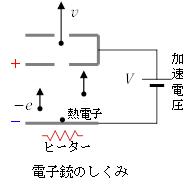
電子を走らせるには，ヒーターで加熱した電極から出た熱電子を一定電圧で加速するという仕組みの電子銃（右図）が使われる。
熱電子の速度はある分布をしているが，いずれにせよ加速後の速度に比べて無視できるくらい小さい。そこで，今の場合は熱電子の速度は0であると考えておいて問題がない。
加速電圧を
とすると，
電子が受ける仕事
が
運動エネルギー
になるので，
(1)
が成り立つ。
磁束密度 の中での電子の円運動の半径は，上記と同様に，
(2)
である。
(1),(2)から
を消去すれば，電子の比電荷
(3)
が得られる。
※サイクロトロン運動の観察から，粒子の電荷や質量を決めることはできないが，比電荷は決まる。
磁場の強さ
，
電子の加速電圧，
および円運動の半径 がわかれば，
(3)式から電子の比電荷 を求めることができる。
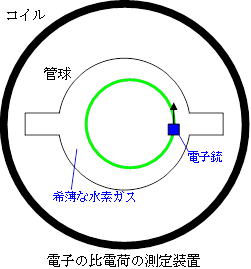
このための実験装置は右図のようなものである。
希薄な水素ガス等を入れた管球中を電子が走ると，電子との衝突により水素分子が緑色の光を出すので，電子の軌道がわかる。
したがって，電子の円運動の半径 が直接読み取れる。
また，磁場の強さ は，
コイルの半径，巻き数，コイルに流す電流などから計算できる。
問 (1)(2)式から，電子の速度 を，
，
，
で表す式を求めよ。