球面上の一様な電荷分布による電界

半径 の球面上に 電荷 が一様に分布している場合の， 中心から距離 の位置での電界の強さを求める。

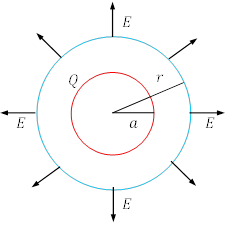半径 の球面を考えると， その表面上のすべての点で，電界の大きさ は等しく， 方向は面に垂直である。
また球面内部の全電荷は であるから， ガウスの定理より，

が成立する。したがって，中心から の位置での電界の大きさは，

となる。つまり，帯電球面の外側の電界は，点電荷の場合と同じである。

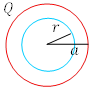次に，帯電球面の内部の電界を考える。

半径 の球面上の各点でも， 電界があるとすれば，それは大きさが等しく，方向は面に垂直なはずである。
このとき，球面内部の電荷は0であるから，ガウスの定理より，

，

したがって， となる。 つまり，帯電球面の内部の電界は0である。