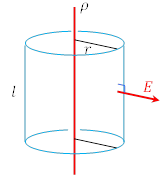
直線上に一様に電荷が分布している場合の電界を，ガウスの定理から求める。
単位長さあたりの電荷密度（線電荷密度）を
として，
直線から距離
の位置での電界を計算する。
そのために，電荷が分布している直線を中心にした 半径，
高さ
の円柱を考え，
その表面からなる閉曲面についてガウスの定理を適用する。
対称性から，電気力線は下図のようになることがわかる。
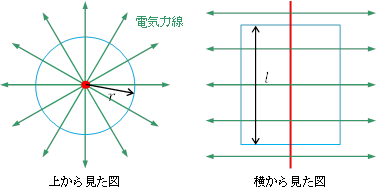
これより，円柱の側面での電界の大きさ
は 側面上ならどこでも等しく，向きは側面に垂直であることがわかる。
また，上下の面上では，電界の大きさは一定ではないが，電界の向きが面と平行になり， 面を貫く電気力線がないので考慮しなくてよい。
この円柱面内の電荷は
であるから，ガウスの定理は，
となり，これより電界の強さは，
のように求めらる。
電荷分布が軸対称の場合は，軸から 離れると，
電界は
の形で弱くなっていく。
