直射日光の当たらない室内にある物体は，気温と同じ温度になっているはずです。
しかし，手で触れると，金属製品は冷たく，木製品は冷たくありません。同じようなことは，洋式トイレにおいて，布製の便座カバーが付いている場合と，カバーがない場合の違いでもっと明確に経験していると思います。
上の例は物体の温度が体温よりも低い場合ですが，逆に物体の温度が体温より高い場合にも似たような現象が起こります。
例えば，50℃の金属には熱くて触れることができませんが，50℃の木材ならば平気で触れることができます。また，気温が100℃のサウナ風呂には入ることができても，100℃の水には入れません（釜茹でじゃ）。
これらの現象は，「接触冷温感」という言葉で語られることがありますが，「感じる」というだけでなく，実際に接触面の温度が違ってくるのです。
ここでは，温度が異なる２つの物体を接触させた瞬間に接触面の温度がどうなるかを，簡単なモデルで考えてみましょう。
温度がそれぞれ
である2物体を
の面で接したとします。
また，物体1，物体2の熱伝導率を
，密度を
，比熱を
とします。
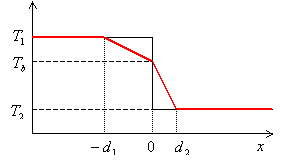
2物体が接触してから，微小時間後の温度分布が，右図の赤い折れ線の形で近似できると仮定します。
接触面の温度を
とすると，物体1側の温度勾配は
なので，物体1から物体2へ単位時間に単位面積を通して流れ込む熱量は，
となります。物体2側でも同様に熱流が書けますが，この熱流は接触面の両側（物体1側と物体2側）で等しいので，
・・・・・・・・・・・・・・・・ (1)
が成り立ちます。
次に，2物体が接触してから図の温度分布になるまでに，移動する熱量を考えます。
図において物体1側の厚さ
の部分では，温度が平均
だけ下がっています。一方，接触面の断面積を
とすると，この部分の体積は
，質量は
ですから，熱容量は
と書けます。
したがって，この部分から流出した熱量は，
になります。物体2側でも同様に流入した熱量が書けますが，これは物体1から流出した熱量に等しいので，
，
すなわち，
・・・・・・・・・ (2)
が成り立ちます。
式(1)(2)の積をとり
を消去すると，
が得られます。ここで，
または
であることに注意すると，
，
したがって，接触面の温度が
･････････・・・・・・・・・・・・・・・・・ (3)
であることがわかります。ここで，
です。
すなわち，接触面の温度は，両物体の温度を
という重みをつけて平均したものになります。
特に，
であれば，
となります。
は単位体積当たりの熱容量ですから，(3)は，
「接触面の温度は，熱伝導率と単位体積当たりの熱容量の積が大きいほうの物質の温度に近くなる」
ことを表します。
いくつかの物質について，これらの量の概略値を示しておきましょう。
| 物質 | 熱伝導率 [W/(m・K)] |
密度 [kg/m3] |
比熱 [J/(kg・K)] |
[J/(m3K)] |
 [J/(m2s1/2K)] |
| 銅 | 400 | 9×103 | 4×102 | 3.5×106 | 3.7×104 |
| 木材 | 0.15 | 7×102 | 〜1.3×103 | 〜9×105 | 〜4×102 |
| 水 | 0.6 | 1×103 | 4.2×103 | 4.2×106 | 1.6×103 |
| 空気 | 0.025 | 1.3 | 1×103 (定圧) | 1.3×103 | 5.7 |
※ここの数値は要確認
人の手の表面近くについて，これらの量がわかりませんが，水と木材の中間程度でしょう。すると，最初に述べた現象がだいたい理解できます。
金属は，熱伝導率が大きいため，接触面の温度は金属の温度に近くなります。
一方，空気は，熱伝導率も体積当たりの熱容量もごく小さいため，空気と他の物体の接触面の温度は，ほとんど物体の温度に近くなります。
最後に念のため注意しておきますが，上記で議論した接触面の温度は，接触直後の温度のことです。一般に，接触後，時間が経つとこの温度は変わっていきます。
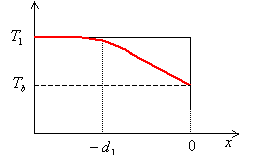
（補足１）
ここで使用した折れ線型の温度分布では，
や
における熱流が保存しません。熱流が保存するには，付近における温度分布は，右図のような形でなくてはいけません。
上記の議論では，この形を折れ線で近似したことになります。
（補足２）
2物体が同じ物質であれば，熱伝導方程式をフーリエ級数によって解けば，温度分布の時間変化がわかります。このとき，接触直後の接触面の温度は，両者の平均温度になります。これは，ギャップがある関数のフーリエ級数の一般論から言えることで，(3)式の特殊な場合になります。
異なる物体の場合も，少し複雑になりますが，同様にして熱伝導方程式を解くことができます。残念ながらまだ数学的な証明ができないのですが，数値的には，接触直後の接触面の温度が(3)式と一致することを確認しています。