は，各位置
，各時刻
で定義でき，一般には
との関数
で表現されます。温度は，各位置，各時刻で定義でき，一般にはとの関数で表現されます。
しかし以下では，簡単な場合として，温度が
とだけで決まる場合，つまり
で表せる場合を考えます。（空間は1次元だけ考えればよい場合）
熱は温度が高い方から低い方へ流れます。
このとき温度差が大きいほど，1秒間に流れる熱量は大きいことが予想できるでしょう。
また温度差が同じでも，物質により流れる熱量は異なるでしょう。
このことを定式化したものが，以下のフーリエの法則です。
単位時間に，単位面積を通って流れる熱量
は，温度の勾配に比例し，
（フーリエの法則）
で表せます。比例定数
は，熱伝導率(heat conductivity)と呼ばれ，物質により決まる量です。
ここで，マイナス符号が付いているのは，熱が高温側から低温側に流れることに対応しています。
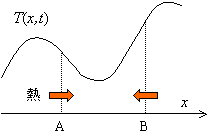
図において，Aの位置では
であり，このとき熱はの正の向きに流れます。一方，位置Bでは
で，熱は負の向きに流れます。したがって，温度勾配の符号と方向に流れる熱量は反対の符号になります。
温度勾配が同じであっても，熱伝導率が大きい物質は多くの熱量を流すので，熱を伝えやすいことになります。
逆に，熱伝導率が小さな物質は，熱を伝えにくいので，「断熱性が大きい」とも言われます。
は単位時間・単位面積当たりの熱量なので，の単位は J/(sec・m2)=W/m2 である。ここで， W(ワット)=J/sec である。の単位は
|
|
※金属の熱伝導率と抵抗率
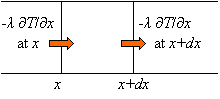まず，単位時間に，単位面積を通って，と
の間にある微小部分に流れ込む熱量を考えましょう。
と書くことにすると，フーリエの法則から，位置の面から流入する熱量は，
，
位置の面から流出する熱量は，
です。したがって，この微小部分に流入する熱量は，
，
すなわち，
･････････・・・・・・・・・・・・・・・・・ (1)
と書けます。
次に，この熱量の流入による温度の上昇を考えます。そのためには，この微小部分の熱容量が必要になります。
断面積を
とすると，この微小部分の体積は
です。物質の密度を
とすると，微小部分の質量は
になります。さらに，物質の比熱（単位質量当たりの熱容量）を
とすると，この微小部分の熱容量は
であることがわかります。
問 
という量はどのような意味を持つか？ （こたえ：単位体積あたりの熱容量）
微小部分の熱容量が与えられたので，時間
の間に断面積を通して流入する熱量と，温度上昇
の関係が次のように書けます。
これに(1)を代入すると，
，
すなわち，
（熱伝導方程式）
が得られます。これを熱伝導方程式といいます。
熱伝導方程式に現れる係数
は，熱拡散率(difusivity of heat)，温度伝導率(temperature conductivity)
，温度拡散率(temperature difusivity) などと呼ばれます。
問 温度拡散率
の単位は？
の単位は，J/(K・kg)×(kg/m3) = J/(K・m3) であるから，
の単位は，W/(m・K)×K・m3/J = m2/s となる。
このことは，熱伝導方程式からもすぐにわかる。
3次元の場合，温度はですが，このときも同様に以下の熱伝導方程式が導けます。
ただし，
一般に，この形の方程式を拡散方程式と呼び，そこに現れる係数を拡散係数といいます。