の計算

まず，を等比級数に展開すると，
　　　　　
となるが，この各項は部分積分により，
　　　　　
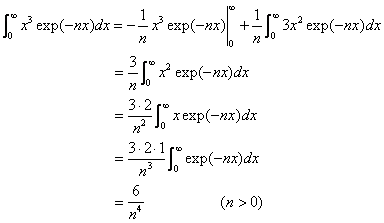
となる。したがって，求める定積分は，

となる。ここで，
　　　　　
という公式を使ったが，気になる人のために，その証明も以下に示す。

の証明

証明のために，次の関数を考える。

　　　　　　　・・・・・・・・・・・・・・　 (1)

これは などで0になることと， であることから，以下のように因数分解できる。

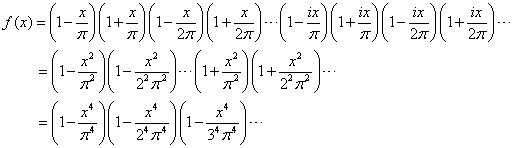
この式のの係数は， である。

一方(1)は，マクローリン展開を使うと，

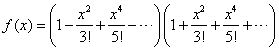
となるので，これのの係数は である。したがって，

　　　　　， 　すなわち，

であることがわかる。

（参考）　 は，ツェータ（ゼータ）関数と呼ばれ， 上の結果は であることを示している。