球面三角法 (Spherical trigonometry)

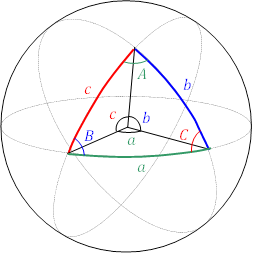
各辺が大円の一部になっている球面上の三角形を球面三角形という。これは地理学や天文学の計算でよく使われ， 平面上の三角形とは異なり，内角の和は180°より大きくなる。

球面三角形 の辺の長さ(大きさ) は大円の中心角で表す。
各頂点と球の中心を結ぶと３つの扇形ができるが，各頂点の内角 は， この扇形の平面間の角を表すことになる。

球面三角形 の 内角 と対辺（中心角） の間には，以下の関係式が成立する。

正弦公式

余弦公式

正弦余弦公式

（注１）と， と を同時に入れ替えた式なども成り立つ。

（注２）角（大文字）と辺（小文字）を入れ替えると，各 の符号を変えた式が成り立つ。

例えば，二辺 と その挟角 がわかっている場合は，

		（余弦公式）
		（正弦公式）
		（正弦余弦公式）

から， と を求めることができる。 は， とした式から得られる。