改良オイラー法 (Improved Euler's method)

運動方程式をとの連立方程式の形に書いたもの
　　　　　，　　
をからまで機械的に積分すると，
　　　　　，　　
となります。

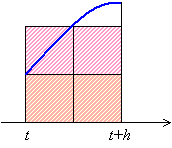
この積分の部分を，
　　　　　，　　
と近似するとオイラー法になります。これは，積分区間の下限での関数値を使っていますが，区間の中央での関数値を使って近似したほうがいいでしょう。すなわち，
　　　　　，　　
とすると，近似がよくなります。

そこで，以下のように計算するのが改良オイラー法です。

(1) まず，とをオイラー法で計算する。
　　　　　

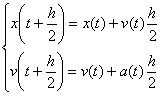
(2) その値を使って，時間が進んだ点の値を計算する。
　　　　　

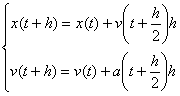
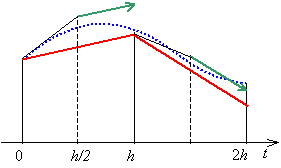
改良オイラー法は，半歩先の微分係数を使って1歩進むということになります。この方がオイラー法よりもずっと正確になることが，図からもわかるでしょう。

以下に，Visual Basic による改良オイラー法のプログラムを示します。
オイラー法の例と同じく，，，という単振動の例で，結果をグラフで表示します。画面の座標は，Scale (-1, 2)-(20, -2) のように設定しておきます。

Private Sub Command3_Click()
    Dim t, x, v
    Dim tt, xx, vv
    Dim h
    
    h = 0.1
    t = 0: x = 1: v = 0     '初期値
    PSet (t, x)
    Do While t <= tmax
        tt = t + h / 2
        xx = x + v * h / 2
        vv = v + a(x, v, t) * h / 2
        t = t + h
        x = x + vv * h
        v = v + a(xx, vv, tt) * h
        Line -(t, x)
    Loop
End Sub

Function a(x, v, t)
    a = -x
End Function

練習3　オイラー法の結果や正確な解と比較してみなさい。

これは，オイラー法でを小さくとる計算法よりもはるかに有効で，演示用のシミュレーションなら改良オイラー法で十分な場合が多いでしょう。

より正確な計算が必要な場合は，ルンゲ・クッタ法などを使います。