ここでは，微分形をした量の体積積分を，その表面上の面積分に置き換えることができる例を示す。
  はスカラー場 |
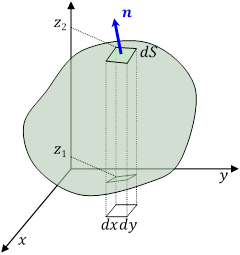
まず，
の 
成分のみを考える。
をある値にしたときの，領域の表面の位置を 
とすれば，
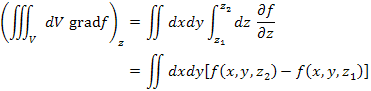
となり，体積積分は表面の関数値だけで書けることがわかる。
さらに，断面積が
の四角柱で切り取られる表面の面積を
とし，この表面に垂直で外向きの単位ベクトルを
とする。
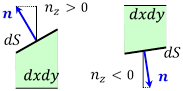
すると，上面(
)では，２つの微小面積 と の間には，
という関係があり，
下面(
)では，
という関係になる。ここで，
は単位法線ベクトル の成分である。
したがって， 
とまとめて書けるので，
となる。
成分も同様な式で書けるので，結局，ベクトルとして，
が成り立つ。
なお，面積素片 を外向き法線の向きを持つベクトル
で表すこともある。このとき 
であるから，
という表記になる。
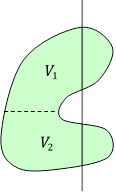
（補足） 体積が右図のような形の場合にも，適切な面で分割して考えれば上と同じ結果が得られる。分割面の面積分は両側で常に反対の符号になり打ち消しあうからである。
浮力
は，静止流体中の物体の表面に加わる圧力
から生じるので，
と書ける。負号は， が外向き法線の方向であるのに対し，圧力により物体が受ける力は内向きであるために付く。
密度
が一定である静止流体中の圧力は，鉛直上向きに軸をとると，
と書ける。ここで，
は重力加速度，
は 
での圧力である。すると，
であるから，
となる。
は物体の体積分の流体の重さであり，これが浮力の大きさになる。（アルキメデスの原理）
また，この式は，浮力の向きは常に鉛直上向きになることも示している。
浮力 の作用線がどこになるかを考える。これには，力のモーメントの合成を考え，
となる位置ベクトル
を求めればよい。この右辺は，先と同様にして，
であることがわかる。ここで，
，
として，上式の
成分を考えると，
， 
であるから，
が得られる。これは，物体が一様な密度であるとしたときの重心位置に等しい。
成分も同様であるが， 成分は決まらない。このように，浮力の作用線は決まるが，作用点（浮心）は決まらない。
これは，物体の各部に働く重力の合成の場合と同様な事情である。
通常は，浮心は物体が排除した液体の重心と一致すると考えておいて問題はない。
  はベクトル場 |
であるから，
であるが，まず右辺の最後の項のみを考える。
先の
の場合と同様に，まず，
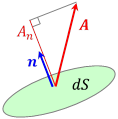
と書ける。次に，表面の微小面積を とし，これに垂直な外向きの単位ベクトルを とすれば，
， 
であるから，
が得られる。
他の項も同様に書けるので，
が得られる。
の外向き法線成分を
とすると，
である。また，面積素辺をベクトルとして と書くこともできる。
したがって，ガウスの発散定理は，
などと書くこともできる。
応用例 電界に対するガウスの定理の微分形
電気のクーロンの法則が
の形であることから，任意の閉曲面
に対して，次のガウスの定理が導かれる。
ここで，
は，電束密度
の外向き法線成分であり，
は閉曲面内にある電荷である。
左辺に発散定理を使い，右辺は電荷密度
の体積積分で表すと，
となる。
は閉曲面 の内部の体積であるが，この閉曲面は全く任意にとってよいので，上式は，
であることを示す。これがガウスの定理の微分形であり，マックスウェル方程式の１つである。