積分により重心の位置を求める

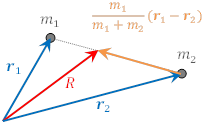
重心の位置ベクトル

位置ベクトル の位置に点状の質量 があり， の位置に があるとき， 重心の位置ベクトル は，２点 を に内分する点であるから，

となる。
３個の質点がある場合の重心も，まず２個の重心に２個分の質量があるとし，それと残りの１個の重心を考えると，全体の重心の位置ベクトルは，

となることがわかる。

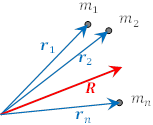一般に個の質点がある場合の重心の位置ベクトルは，

となる。ここで は全質量である。

問　個の質点がある場合の重心の式を数学的帰納法で証明せよ。

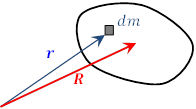大きさを持った物体も，それを多数の小片に分解して考えると，質点の集まりと考えることができる。
実際には，連続した物体を無数の部分に分けてその和をとるので，積分計算になる。

位置 における物体の密度を とすると，
その位置の微小体積 の質量 は である。

全質量は，

であり，重心の位置ベクトルは，

と表せる。ここで積分の範囲は物体の全体積 をカバーするようにとる。

（注） 実際の積分は成分ごとに計算することになる。例えば， の成分 は，
　　　　　
となる。

例題

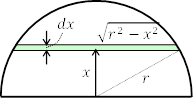例題１　半径 の一様な半円板の重心

板の場合は2次元で考えてよいので，密度 の代わりに面密度 を考えればよい。（板の厚さを とすると， という関係になる。 ）すると，全質量は である。

右図の位置にある幅 の棒状の部分の質量は， であるから，重心の位置 は，

となる。ここの定積分の値は であるから， と計算できる。

（参考） の計算は， と置換すればできる。
であるから，この定積分は
　　　　　
のように計算できる。

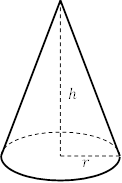例題2　一様な物質でできた，底面の半径，高さ の円錐の重心

底面から の位置で厚さ の円板を考えると，その半径は であり，その体積は となる。これより重心の高さ は以下のように計算できる。

問　一様な物質でできた，半径 の半球の重心の位置を求めよ。

（こたえ）　

※これは半円板のときの より大きいか，小さいか？
　そのことが直感的にわかるか？

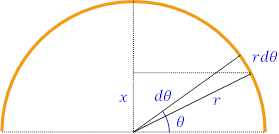例題3　半径 の半円環の重心

線状の物体に対しては，密度の代わりに線密度 を使えばよい。すると，全質量は である。

このような問題は，曲座標で計算すれば簡単になる。
図のような角度 と の間にあるリングの部分の質量は である。重心は図の中心線上にあるので，円の中心からの距離 だけを考えればよい。 を 0 から の範囲とすると， の位置の質量は両側にあるので の重みを付けなくてはならない。

このように考えると，重心の位置 は，次のように計算できる。

※これは半円板のときの より大きいか，小さいか？
　そのことが直感的にわかるか？