先に，座標系が並進運動している場合の慣性力を考えたが，座標系が回転していると別な慣性力が現れる。
座標系が回転しているときの慣性力には，遠心力とコリオリ力があるが，ここではまず遠心力を説明する。
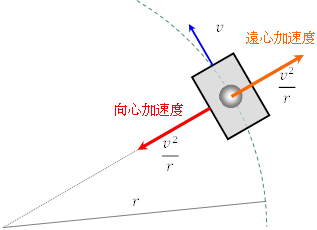
自動車が急カーブを曲がるときに，中の人や物はカーブの外側向きに見かけの力を受ける。これが遠心力である。
自動車が半径
のカーブを速さ
で走っているとき，自動車の加速度はカーブの中心向きに 
である。（向心加速度）
車の中の人や物は速度 で直進しようとするが，車がカーブの中心向きに速度を変えるので，車の中で見ると人や物は外向きに速度を変えるように見える。この見かけの加速度の大きさは
である。
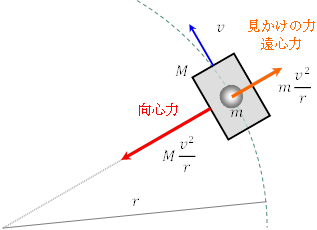
車の向心加速度 は，タイヤと道路の摩擦力により与えられており，その大きさは車の質量を
とすると，
である。（これが向心力）
一方，車の内部の人や物には，座席との摩擦力を無視すれば，実際には水平方向の力は働いていない。しかし，車の中で観察すると，外向きに大きさが の加速度が働くので，車中の人または物の質量を
とすると，外向きに 
の力が働いているように見える。この見かけの力が遠心力である。
速度 を角速度
で表すと，
であるので，遠心力は 
とも書ける。
遠心力（見かけの力）
遠心力は見かけの加速度から生じる力であるから，力の大きさは質量に比例する。
直線運動の場合の慣性力のところでも述べたが，質量の大きなものは動きにくい（倒れにくい）という常識は，車の中の遠心力に関しては通用しない。
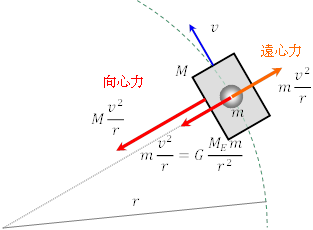
質量 の人工衛星が，地球の周りを半径，速さ の円運動をしているとする。
先と同様に，人工衛星の向心加速度は で，向心力は である。
今度の場合，この向心力は万有引力 
により与えられている。
（ここで，
は万有引力定数，
は地球の質量である。）
(1)
人工衛星内の質量 の物体（または人）も円運動をしており，その向心力は万有引力による。
(2)
人工衛星の内部で見れば，質量 の物体は遠心力 を受けるが，これが向心力（＝万有引力）とつりあうので，無重力状態になる。
もちろん，実際に働いているのは万有引力のみで，人工衛星も中の物体も万有引力で円運動をしているだけなのであるが，内部で見ると，遠心力により重力が打ち消されたことになる。
そのため，(2)式は，人工衛星内部での遠心力と万有引力のつり合いの式と見ることもできる。
一方，人工衛星に対する(1)式は，向心力が万有引力により与えられるという関係を示すものでしかない。
物理の問題集などで，(1)の説明として「人工衛星に働く遠心力と万有引力のつり合い」という表現が使われることがある。しかし，遠心力は慣性力（見かけの力）であり，それを生み出す座標系が必要である。この座標系は人工衛星と共に動いている座標系になる。
このような座標系は人工衛星に対しては自然なものではないので，「遠心力と万有引力のつり合い」という表現は避けた方がよいと思われる。実際，教科書などには，この表現はまず見られない。
※人工衛星の内部の座標系が人工衛星と共に動いている座標系ではあるが，この座標系から人工衛星を眺めることは自然ではない。
向心力よりも遠心力という言葉の方が一般に馴染みが多い。自動車の運転教則本などにも「カーブを走るとき自動車は遠心力を受ける」と書かれてある。
上の人工衛星と同じで，車に対しては遠心力という言葉は使わない方がよいように思うが，運転手は実際に車が外向きに引かれるという感じを受けることがある。
運転手は，道路に沿って動く座標系をイメージしているので，その座標系では確かに自動車に遠心力が働くことになる。
洗濯機における脱水の際や，犬や猫が水に濡れたときに身を震わせて水滴を飛ばす際にも遠心力が使われている。いずれの場合も，水は円運動の接線方向に飛び出すが，回転している座標系から見ると，水は遠心力で外側に飛び出していくことになる。
血液などの試料に大きな遠心力をかけて，資料の成分を分離することを遠心分離といい，その装置を遠心器（遠心分離器）という。モーターで高速回転させると地上の重力の数千〜数万倍という遠心加速度が出せるので，通常なら分離困難な試料も，わずかな密度差があれば分離できる。
問 上図で，
のとき，遠心加速度が 
となる角速度 を求めよ。
（
は重力加速度 
のこと。）
（こたえ） 
より，
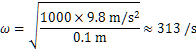である。
ちなみに，このとき毎秒の回転数は 
となる。
