運動方程式 ![]() から
から![]() であるが,物体の質量
であるが,物体の質量![]() は変化しない定数であることが多い。その場合は,
は変化しない定数であることが多い。その場合は,
![]() ・・・・・・・・・・・・・・・・・・・ (1)
・・・・・・・・・・・・・・・・・・・ (1)
とも書ける。ここに現れる,![]() を運動量 (momentum) という。運動量はベクトル量である。
を運動量 (momentum) という。運動量はベクトル量である。
物体の運動量 = 物体の質量
× 物体の速度
,
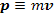
(1)式は,「力に無限小時間を掛けたものは,その間の運動量の無限小変化に等しい」ことを示している。
有限の時間を考えるには,これを積分することになる。
時刻![]() の速度が
の速度が![]() ,時刻
,時刻![]() の速度が
の速度が![]() だとすると,(1)を
だとすると,(1)を![]() から
から![]() まで積分して,
まで積分して,
![]()
となる。この左辺の量を力積 (impulse) という。力積という言葉を使うと,
物体の運動量は,受けた力積の分だけ変化する。
ということができる。
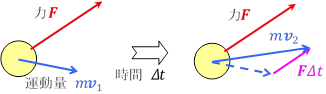
特に,時刻![]() から
から![]() までの間,力
までの間,力![]() が一定であるなら,
が一定であるなら,![]() として,力積は,
として,力積は,
![]()
と書ける。
 1方向(例えば
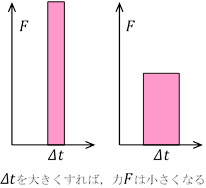
1方向(例えば![]() 方向)の運動だけを考えると,力積は右図の面積になり,これが運動量の変化に等しい。
方向)の運動だけを考えると,力積は右図の面積になり,これが運動量の変化に等しい。

力が時間とともに変わる場合も,同様で,力積は右図の面積になる。

定義からわかるように,力が作用する時間が短ければ,力積は小さくなる。時間がごく短ければ,力積も無視できるほど小さく,したがって運動量もほとんど変化しないのが普通である。
しかし,力が作用する時間が短くても,その力が非常に大きければ力積は目に見える効果をもつ。このように,ごく短時間だけ作用する大きな力を撃力という。
例えば,野球のボールとバットが接している時間は1/100秒程度で,この間しか力は働かないが,その力は撃力であり,ボールの運動量は大きく変化する。
一般に,2つの物体が衝突する場合に働く力は撃力になる。
例1 だるま落とし
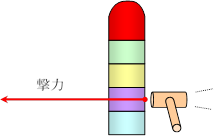
だるま落としは,慣性の法則の例として取り上げられることが多い。つまり,力を受けない(撃たれていない)物体は,そのまま動かないという説明になるわけだが,実際には,摩擦力のため撃たれていない部分も動く。
摩擦力まで考えると,だるま落としは,力積の例として最適である。
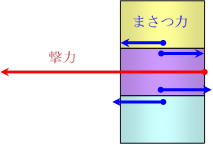
撃力を受けた物体は動き出すが,その上下の物体との間に左図のように摩擦力が働く。そのため,上下の物体も同じ方向に動こうとする。
だるま落しが成功する理由は,摩擦力が撃力ではなく,普通の大きさの力であることによる。つまり,摩擦力が働く時間を短くすれば,それに比例して摩擦力による力積を小さくすることができ,上下の物体への影響を小さくできる。
したがって,だるま落しを成功させる方策は,物体が擦れあう時間を短くすること,つまり,たたいた物体をできるだけ高速に走らせることに尽きる。(そのためには,槌も重たいものの方がよい。)
○ガラスコップの上にトランプのカードを置き,さらにその上に硬貨を置く。カードを勢いよく弾くと,硬貨はコップの中に落ちる。
○食器を乗せたテーブルクロスを抜き取る。
例2 緩衝(クッション)
キャッチボールでボールを受けたときに,その手を後ろに引くようにすると衝撃が和らぐのは経験しているだろう。
一定の運動量を持って飛んできたボールを止めるには,その運動量と同じ大きさの力積を加えなくてはならない。
同じ力積を与える場合でも,力を加える時間を長くすれば,力は小さくてすむ。
ボールを受けたときに手を後ろに引くのは,力を加える時間を長くすることになっている。
ガラスコップをコンクリートの床に落とすと割れるが,やわらかい材質の床なら割れないことがある。
衝突時の力が加わっている時間が1/100秒であるのと,1/10秒である場合を比べると,力の大きさは約10倍も違ってくる。
問 自動車には,衝突時の衝撃を緩和するためにどのような工夫がされているか?
※緩衝については,次の「仕事と運動エネルギー」の項も参照。