質点系の力学

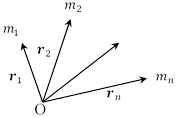
大きさを持つ物体も小さな部分に分解すれば質点の集まりとみなすことができる。

そこで，個の独立な質点からなる系を考えることにし，各質点の質量と位置を，，各質点に加わる力を（）とする。

番目の質点に働く力は，さらにのように分けて考えることができる。は質点系の外から番目の質点に働く力（外力）であり，は番の質点が番の質点に及ぼす力（内力）である。

ここでは，外力だけに依存する重要な結果を説明する。

まとめ

まず，結果だけをまとめると以下のようになる。

重心の位置ベクトルを，全質量をとすると，全運動量はであり，
　　　　　　　　　　　　　(1)
が成り立つ。右辺の力は，質点系に対して働く外力の和である。

全角運動量に対しては，
　　　　　　　　　　　　　(2)
が成り立つ。右辺のは，質点系に働く外力によるトルクである。

また，重心が動いていても，重心に関する全角運動量と全トルクについては，
　　　　　　　　　　　(3)
が成り立つ。

このように，質点系全体を考えれば，質点の場合と同じ形の方程式が成り立つ。

以下に，それぞれの導出計算を示す。

全運動量

各質点の運動方程式の和をとると，
　　　　　　　　　　(4)
となる。

(4)の左辺は，重心（=質量中心）の位置ベクトルを使うと，
　　　　　
と書ける。ここで，は，質点系の全質量である。

(4)の右辺に関しては，まず力を外力と内力に分けて，と書く。は番の質点が番の質点に及ぼす力であり，作用・反作用の法則によりという関係がある。すると，右辺の和において，内力の部分は必ずペアで打ち消しあうので，
　　　　　
となり，外力のみの和になる。

したがって，(4)は，
　　　　　　　　　　(5)
となり，質点系の全質量，重心の加速度，外力の和に対しては，1つの質点と同じ形の運動方程式が成り立つことがわかる。つまり，重心の運動は，力としては外力だけを考えて，質点の運動と同様に扱えるということである。

例１　体重の人がジャンプした場合，外力は重力だけであるから，ジャンプ後どのように姿勢を変えても，重心は放物運動をする。ジャンプ後に姿勢を変えると，身体の各部分に内力が働くが，これは重心の運動には無関係である。

例２　（空気抵抗を無視すれば）花火や爆弾が空中で爆発した後も，その重心の軌跡は放物線を描く。

全運動量を使うと，(5)は，
　　　　　　　　　　(1)
となる。質点系の全運動量の時間的変化率は外力の和に等しく，特に，外力の和が0なら全運動量は保存する（運動量保存則）。

問　全質量がである静止した質点系がある。その中の１つの質点に撃力を加えて運動量をにしたとき，質点系全体の重心の速度を求めよ。
　　　（こたえ）質点系全体の運動量もであからである。したがって，である。

全角運動量

各質点の運動方程式に，左からをベクトル的に掛けて和をとると，
　　　　　　　　　　(6)
となる。

(6)の左辺の各項は各質点の角運動量の時間微分であるから，左辺の和は全角運動量の時間微分を表す。

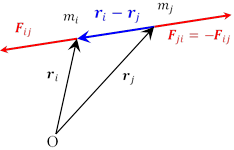
(6)の右辺の内力に関する部分は，質点の対のすべての組み合わせに対して和をとることになる。
この中の任意の対について，作用反作用の法則から，
　　　　　
が成り立つので，内力が相対位置ベクトルと平行であれば（注1），これは0となる。したがって，それらの和も0となる。

結局，(6)は
　　　　　　　　　(2)
となり，質点系の全角運動量の時間的変化率は外力による回転力の和に等しい。

特に，外力のモーメントの和が0のときには，全角運動量は保存する（角運動量保存則）。

（注1）内力が相対位置ベクトルと平行でないときは，偶力を生じることになる。しかし，質点系全体に対して偶力を生じることはなく，(2)はより一般的な「空間の等方性」という仮定から導ける。

重心に関する角運動量とトルク

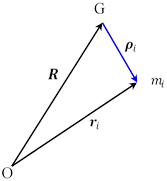
最後に，(2)式を重心に関する角運動量やトルクで書き換えてみる。
そのために各質点の位置ベクトルを
　　　　　
と書く。は重心から見た各質点の位置ベクトルである。

(2)の右辺のトルクは，
　　　　　　　　　　(7)
となる。ここでは外力の和である。第２項は重心に関するトルクである。
すなわち，全トルクは重心に全外力が働いたとするトルクと重心に関するトルクの和になる。

次に，，したがって，であることを使うと，全角運動量は
　　　　　
となる。ここでは全運動量である。第２項は重心に関する角運動量である。
すなわち，全角運動量は，重心運動の角運動量と重心に関する角運動量の和になる。

これをで微分して，
　　　　　
を得る。ここで，とは平行なのでであることを使った。

さらに(1)を使うと，
　　　　　　　　　　　　　　　　　　　　　(8)
となる。

(2)と(7),(8)式から，
　　　　　　　　　　　　　　　　　　　　　　　　　　(3)
が得られる。これは，重心が動いていても成立する式である。

「重心の運動エネルギー」

(5)式
　　　　　
は，質点の運動方程式と同じ形であるから，質点の場合の仕事と運動エネルギーの関係（運動の第2積分）と同じものが以下のようにして得られる。
両辺と重心の速度の内積をとると，
　　　　　
となるから，
　　　　　
を得る。
は全質量が重心に集中したときの運動エネルギーであるから，「重心の運動エネルギー」と呼んでもよかろう。一方，は外力による仕事とは言えない。は重心の移動距離であり，外力の作用点の移動距離ではないからである。しかし，外力と重心の移動距離の内積が「重心の運動エネルギー」の増加になることは，一般に成り立ち，日常現象への応用にも便利なことが多い。