ここでは剛体の回転軸を
軸として，角運動量の 成分以外の成分も考える。
このときは，角速度もベクトル
と考えると便利である。
の大きさは
であり，剛体が回転する向きを右ねじが回る向きとしたときに右ねじが進む向きをベクトル の向きとする。
このように角速度ベクトルを定義すると，剛体中のある一点（位置ベクトル
）の速度
は，
というベクトル積で表せる。
この位置の質点の質量を
とすると，角運動量
は，
となる。（最後の変形がわからない人は，ベクトル積のページを参照のこと。）
，
を使って，全角運動量
の 成分を書くと，
となる。ここで，
は軸に関する剛体の慣性モーメントである。
軸の周りの回転の場合，慣性モーメント
は時間によらない定数になる。
同様に，全角運動量の
成分を書くと，
となる。ここで，
を慣性乗積という。
軸の周りの回転の場合，
は一定だが
は時間とともに変化する。そのため一般に慣性乗積も時間に依存する。
しかし，座標系をうまくとればすべての慣性乗積を0にすることができる。
これは，線形代数の，「実対称行列は直交行列で対角化できる」という定理で表される内容である。
（複素数の場合も含めると，「エルミート行列は，ユニタリー行列で対角化できる」と表現される。）
直交行列は座標系の回転に対応している。詳しくは，力学の教科書を参照のこと。
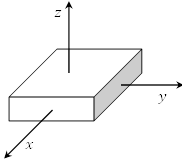
対称性をもった剛体の場合は慣性乗積が0になる座標系がすぐにわかる。
例えば，直方体で一様な密度の剛体であれば，図のように
軸をとれば慣性乗積は0になる。このような３つの軸を慣性主軸という。
じゃがいもの形のように対称性がない場合も，必ず３つの互いに直交した慣性主軸が存在する。
回転軸を慣性主軸の向きにとったとき，これらの軸に関する慣性モーメント
を主慣性モーメントという。
このとき，回転軸が任意の方向を向いていても，角速度を
とすると，全角運動量の各成分は，
， 
， 
のように簡単に書ける。
慣性主軸で回転させると，軸に垂直な方向の角運動量は0であり，その方向のトルクも働かない。
そうでない場合は，軸に垂直な向きにもトルクが作用し軸を固定しにくい回転になる。