実際に，球を斜面上で転がせると，なかなかまっすぐには転がらず苦労するだろう。
そのときは，右図のような浅く広い溝の中を転がらせるようにすればよい。
この場合，斜面上で静止していた球が，高さ
だけ滑らずに落下したときの速度
は，力学的エネルギーの保存則，
（注）右辺第2項は回転の運動エネルギー 
より，
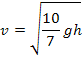
になる。
これは，回転を無視したときの値
の85%程度になる。
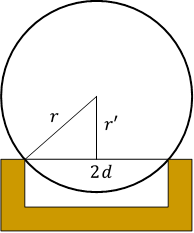
断面がゆるく湾曲した斜面のかわりに，コの字型のレールもよく使われる。
球の半径を
，溝の幅を
とすると，摩擦力によるトルクを考える際の腕の長さは，
となる。
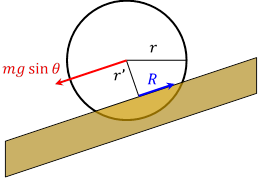
運動方程式
， 
および，滑らないという条件
から，前と同様に，加速度は
となる。
慣性モーメント
は，球の半径 を使って，
であるから，
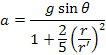
となる。
であるから，この加速度は平面を転がる場合よりも小さくなる。
特に，すなわち
のときは加速度が0になる。これは球を平行な板で挟んだ場合に相当する。
この場合も力学的エネルギーは保存するので（証明はこちら），静止状態から だけ下がったときの速度は，
より，
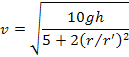
となる。これは，
よりさらに小さくなる。
微小時間
の間のエネルギー変化を考える。
この間に物体は斜面に沿って
だけ進み，高さは
だけ下がったとすると，
， 
， 
などの関係がある。
すると運動エネルギーの変化は次のように書ける。
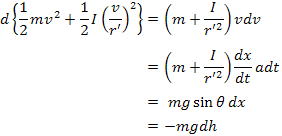
したがって，力学的エネルギーが保存することがわかる。