剛体壁ポテンシャル

通常の引力のポテンシャルを単純化したものが井戸型ポテンシャルで，それをさらに単純化したものが剛体壁ポテンシャルである。
粒子がいかに高いエネルギーでぶつかっても跳ね返されることになる。

シュレディンガー方程式は，
　　　　　　　　　　(1)
である。

および の部分では，ポテンシャルエネルギー が無限大になっているとすると，ここでは しか解はない。

では， であるから，シュレディンガー方程式(1)は，
　　　　　
となる。この2階微分方程式の一般解は，

　　　　　　　　　　　　(2)

である。ただし， は定数であり，
　　　　　　　　　　　　　　　　　　　　(3)
である。

一般解(2)は， および の部分の解 と連続でなくてはならないので，
　　　　　
でなくてはならない。

を(2)に代入すると， となる。さらに， より であることがわかる。
したがって，
　　　　　 　すなわち，　　　　　 (4)
でなくてはならない。ここで は整数である。

したがって，波動関数は，
　　　　　
となる。 は整数であるが， のときは と同じ波動関数であり， のときは となり，この状態はないことになるので，結局 という自然数だけになる。

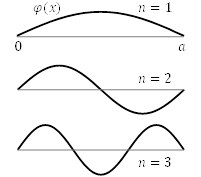
この波動関数は，両端が固定された弦の基本振動，2倍振動，・・と同じ形をしており，右図のようなのものになる。 が1つ増えると節が1つ増える。

波動関数の二乗である粒子の存在確率も が1 増えると，山が1つ増える。
が非常に大きくなると，一様な分布に近づいてくるが，これが古典論での存在確率（粒子の速さは一定であるので， の範囲に一様な確率で存在する）に対応している。

この波動関数の波長 は， であるから，(4)の は すなわち伝播数を表している。これは運動量 に対応するので，全エネルギーは，

　　　　　　　　（）

となる。

このようにエネルギーは離散的になるが，プランク定数はマクロな感覚では0に等しいほど小さい数なので，粒子の質量 やポテンシャルの幅 が，1g や 1mm といったマクロな量のときはエネルギーが離散的であることは観測できない。

エネルギーが離散的であることがわかるのは， が電子の質量， が原子や分子のサイズといったミクロの量である場合に限られる。

古典論は， や がマクロな量であるためエネルギーがほぼ連続的であり，その中で が非常に大きい状態に対応する。
（より正確には， が非常に大きい状態を多数重ね合わせた状態に対応する。）

また，最低エネルギーは 0 ではないことに注意しよう。
もし粒子が完全に静止しておれば，運動量は0 であるから，その不定さ も 0 になる。すると，不確定性原理から位置の不定さ は無限大になるはずだが，粒子は の範囲にあるはずだから であり矛盾する。

逆に であれば，少なくとも でなくてはならない。したがって，ポテンシャルの（端では0であってもよいが）中では でなくてはならない。これより，
　　　　　
となる。この式は先の と同じ程度の大きさである。すなわち，最低エネルギーは不確定性原理によってその大きさが制限されてくる。

問　波動関数 を規格化しなさい。
　（こたえ）　　　これが，1 となるように とすればよい。