運動する物体（質点）の世界線が 
であるとする。物体の速度が光速度より小さければ，パラメータ
としては世界線の長さがとれる。世界線の長さは，前述のように，
という不変量から定義される。
は，ニュートン力学における物体の軌跡 
（
）に対応するものである。
パラメータを ではなく，固有時
に変えてもよい。固有時 は，
， または 
で定義される。 光速度
が座標系によらないので， も不変量である。
であるから，
または， 
（ 
）
という関係になる。ここで，
は通常の速度 
（）で， 
は速度の絶対値である。
物体と共に動いている座標系では，
であり 
となるから，固有時は物体と共に動いている座標系での時間という意味がある。
以下では，物体の世界線が 
であるとする。
ニュートン力学の速度を拡張して，ミンコフスキー空間のベクトルとするには，
（
）
で速度を定義すればよい。これを，４元速度（four-velocity）という。
はローレンツ変換の不変量であるから，これが４元ベクトルであることがわかる。
空間部分（）については，
すなわち 
であるから，
のときは，通常の速度
と一致する。
一方，第0成分は，
である。
なお，４元速度の大きさ（長さ）の２乗は，
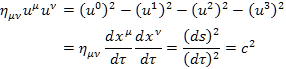
という定数になり，４つの成分は独立ではない。
４元加速度を 
で，４元運動量を 
で定義する。
は物体の質量で不変量である。これらも明らかに４元ベクトルである。
さて，ニュートンの運動方程式は，
すなわち 
（ ）
である。ただし，
はニュートン力学の運動量である。
これを一般化した特殊相対論の運動方程式は，
または 
（ ）
となる。ここで，
は４元力である。
４元力が何者であるのかはすぐにはわからないが，物体の速度が遅くなればなるほど 
（ ）は通常の力
に近づくものでなくてはならない。特に，（瞬間的に）物体と同じ速度で動く座標系で見ると，物体は静止しており，このときは正確に 
とならねばならない。このとき第0成分は，
であるから，
である。
物体の静止系で の全成分が与えられたので，物体が動いて見える座標系へローレンツ逆変換すれば，一般的な結果が得られる。
物体が動いている座標系では，
であるから，
， 
（ ）
となる。ここで，ニュートン力学的な力を 
で再定義した。物体が動いている座標系では
すなわち 
であることになる。
また，第0成分は，
であるから，
， 
であるが，
は次のように求めることもできる。
の両辺を で微分すると，
（４元速度と４元加速度は直交する） が得られるが，これに を掛ければ，
となる。すなわち，
となる。
一方，
はエネルギーと関係していることが以下のようにしてわかる。
より，
であるから，
である。右辺は仕事であるから，
がエネルギー
である。
結局，特殊相対論のエネルギーと運動量は，
，
となる。ここでは，相対論的な質量
を使っている。これに対して， のことを静止質量（または，固有質量）ということがある。
より，
すなわち，
という関係がある。特に，光子のように静止質量 が 0 の粒子では，
という関係になる。
粒子の速度 が小さいときには，
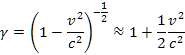
であるから，
，
となり，静止エネルギーと呼ばれる
の項を除くと，ニュートン力学の表式に帰着する。