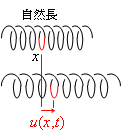
ばねを伝わる縦波の変位
は，波動方程式
(1)
を満たす。縦波の速さ
は，ばねの弾性定数
，自然長
，線密度
を使って，
で与えられる。（導出はこちら。）
ばね全体の質量
を使うと，
と書くこともできる。
ここでは，
は固定端，
は自由端である場合を考える。境界条件は，
(2)
(3)
また，ばねに働く重力は無視する。これは摩擦のない水平な台の上に，ばねを水平に置いて振動させる場合に相当する。
一般解 
に対して，(2)の境界条件を使うと，
(4)
すなわち，後退波と進行波のグラフは原点に関して点対称になることがわかる。
また，(3)より，
， すなわち 
となる。
積分すると，
であるが，定数は
に含めて
(5)
としてよい。これは進行波と後退波のグラフが に関して線対称であることを示す。
(4),(5)より，
， 
であることもわかる。
ここで，具体的な初期条件として，
， (6)
(7)
とする。
(７)より，
，すなわち，
，(5)で とおくと，この定数は0であり，
となることがわかる。
(6)からは，
が得られる。
上記より，
は，奇関数で， に関して対称であり，
周期の関数であるから，初期の変位
が与えられれば，全領域で が決まる。
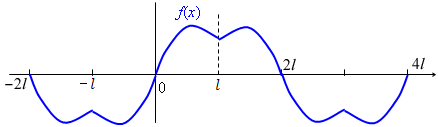
この を使って，変位は，
と書ける。
具体例 水平に置かれたばねの自由端を
だけ引き，ばねを一様に伸ばした状態で手を離した場合
初期変位 から は，図の形になることがわかる。
その後の各点の変位は下図のように求められる。
この変位は，両端が固定された弦を中央で弾いた場合の，弦の一端から中央までの変位と同じ形である。
もちろん，今の場合は縦波であるので，ばねの振動の様子をイメージするには少し想像力が必要となる。
言葉で説明すると，
(1) 自由端から順に縮んでいき，自然長になる。
(2) 固定端から順に縮んでいき，ばね全体が縮む。
(3) 自由端から順に伸びていき，自然長になる。
(4) 固定端から順に伸びていき，最初の状態に戻る。 この繰り返し。
シミュレーションソフト →
なお，自由端の位置の時間変化は下図のようになり，その周期は，
である。
