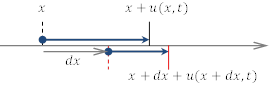
縦波の変位について（補足）

縦波の場合，位置 の変位が であれば，この点は の位置に移動していることになる。

同様に，その近くの の点の変位は であるから，この点は の位置に移動している。

この２つの位置の差は，

となる。
この部分は，本来 の長さであったから，この部分の伸びは， となる。（これが負なら縮みを表す。）

伸びと元の長さの比をひずみというが，今の場合，ひずみは，　となる。

のときは，その部分は伸びでおり， のときは，縮んでいる。

さて，変位後の２点が元の並びと入れ替わることはない。

のとき，この条件は， となる。すなわち，

でなくてはならない。 のときも同じ条件になる。これは，縮みには限度があることと対応している。
これは，ばねの場合，いくら縮めてもばねの長さは正であり，負にはなれないことに対応している。

正弦波 の場合，

であるから， より， すなわち，

となり，縦波の場合には，振幅と波長の間にはこの制限が付く。