弦の横波の場合は,横軸を位置 x,縦軸を各xにおける変位とするグラフがそのまま弦の形になるので理解が容易です。
縦波(粗密波)の場合には,同じグラフをグラフを描いても,それが媒体の形とは直接結びつかないため,グラフを理解することが少し難しくなります。
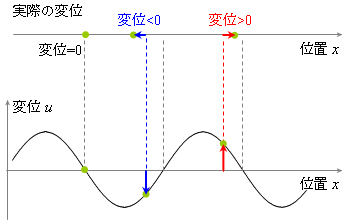
縦波の実際の変位とそのグラフ表示の関係は下図のようになります。
下のプログラムは,縦波のグラフ表示がどうなるかを示すものです。
| 上段 | 媒体内各点の実際の変位・・・粗と密の部分が見るだけでわかります。 |
| 中段 | 横軸を位置 x,縦軸を変位としたグラフ・・時間とともにグラフの形が変わります。 |
| 下段 | 横軸を時間 t,縦軸を変位としたグラフ・・上の赤い点の変位の時間変化を示します。 |
(参考)上段を無視して,中段を横波の実際の様子と見ることもできます。
その場合,中段はそのまま,横軸を位置 x とした変位のグラフとみることができます。
下段は,横軸を時間 t とした,赤い点の変位のグラフです。
波形1 は,正弦波です。まず,この場合だけを見ましょう。
このとき,密の位置は,中段と下段のグラフのどこに対応するか観察しなさい。
進行波と後退波の場合で,これは違ってくるかも観察しなさい。
問 なぜそうなるのかを考えなさい。
波長や振動数を変えると,中段と下段のグラフはどのように変わるか観察しなさい。
問 なぜそうなるのかを考えなさい。
オシロスコープで音波を観察すると,下段のグラフの一部分を切り出したものが見えます。