を簡単な導出法で示す。水の波は表面波と長波に分けられる。 また波動の元になる復元力，すなわち表面を平らにしようとする力には，重力と表面張力がある。ただし，表面張力は表面波のときのみ効果を現す。
ここでは，それぞれの水波の速さ を簡単な導出法で示す。
表面波は表面付近だけが振動している波であり，水面から下にいくと急速に振幅は小さくなる。ここでは，表面の各点が等速円運動をしているトロコイド波を考える。
表面の各点は半径
の円運動をしており，その振動数を
とすると，各点の速さは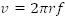
である。波の速度を，波長を
とすると，
であるから，
(1)
である。
この波を，波の速度 と同じ速度で進む観測者から見ると，下図のように，水面の形は変化せずに水は後方へ流れていくことになる。
この流れは定常流であり，水面は流線の１本になる。また，水面の圧力はどこでも大気圧と考えてよい。したがって，ベルヌーイの定理より，
， すなわち
(2)
が成り立つ。ここで，
は水の密度，
は重力加速度である。
式(2)に(1)を代入すれば，
，したがって波の速さは次式で表せる。
（重力表面波の速さ）
ここでは復元力として重力のみを考えたので，これを重力表面波という。
これを，振動数で表すと，
より， 
となる。
波長がごく短いときには，復元力として表面張力も効いてくる。ベルヌーイの定理において，表面張力による圧力変化も考慮すれば，表面波の速度は次式になる。
（表面波の速さ）
ここで，
は水の表面張力， は水の密度である。
波長が数cm以上あれば第1項の重力表面波が主になり，波長が1cm以下の「さざなみ」であれば第2項の表面張力波が主になる。
問 水の表面波の速度が最も小さくなる波長を求めよ。
水深
に比べて，波長が十分長い波を長波という。表面波とは異なり，水底近くまで水の変位は大きい。
表面が楕円振動をしているとすると，水面から深くなるにつれて，水の変位はより扁平な楕円振動になる。（縦波に近い波動になる。）
この波を，波の速度 で進む観測者から見ると，水面の形は不変のまま，水が後方に流れていくことになる。
表面は流線になるのでベルヌーイの定理が使える。表面の鉛直方向の振幅を とすると，表面波の場合と同一の式が得られる。
また，定常流であるので，単位時間にAの断面を通過する水量とBの断面を通過する水量は等しい。（この関係を「連続の式」という。）これより，
， すなわち
(4)
が得られる。
(3), (4) より，
，すなわち，
（重力長波の速さ）
が得られる。波の速さは，水深の平方根に比例する。
例 地震に伴って発生する津波は重力長波である。平均水深 
である太平洋や大西洋を伝わる津波の速さは，
となる。時速に換算すると 
であり，ジェット機並の速さである。
問 水深が 
，
，
のときの津波の速さを求めよ。
問 遠浅の海岸での波は，海岸線に平行に打ち寄せるのは何故か。
（一方，水泳プールの波は，壁に平行にはならない。）
