が小さいという近似をすれば，次の波動方程式を満たす。さまざまな波動の変位は，変位が小さいという近似をすれば，次の波動方程式を満たす。
・・・・・・・・・・・・ (1)
ここの定数
は波の速さを表すことが，以下の一般解(2)からわかる。
※変位はベクトルだが，その各成分が(1)を満たす。
（参考）３次元の波動方程式
3次元の場合，変位はとなり，波動方程式は以下のようなる。
波動方程式(1)の一般解は，
・・・・・・・ (2)
となる。ここで
は任意の関数である。（証明はこちら）
は 
の正の向きに，
は の負の向きに，速さ
で進む波を表すので，それぞれ，進行波，後退波と呼ばれる。
波動方程式の一般解は，任意の進行波と後退波の重ね合わせになる。
この一般解は，ダランベール（d'Alembert）の解と呼ばれる。
補足説明 が の正の向きに速さ で進む波を表すことは，次のようにしてわかる。
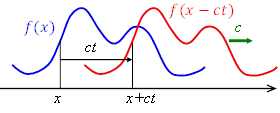任意のについて，の
における値は
のにおける値と等しくなる。したがって，はをの正の向きに
だけ平行移動したものである。
時間が
経過すると だけ移動するので，その速さは になる。
同様に， は，
を の負の向きに速さ で平行移動したものであることがわかる。
，
とおき，変数を
から
に変換する。
，
同様に，
であるから，波動方程式(1)は，
すなわち，
と書けることがわかる。
から，
は
に依存しないことがわかるので，
と書ける。ここで，
は任意の関数である。これを，
で積分すると，
となるが，積分定数
は， には依存してよい。
したがって，
となり，波動方程式(1)の一般解が(2)であることが証明できた。
