の領域の波動を考えるとき，
での境界条件として最も簡単なものとして以下の２つがある。現実の問題では，波動が無限の彼方まで伝わることはまれで，あるところで媒質の状態が変わるのが普通である。
その場合，媒質の状態が変わる場所で，変位がどのような振る舞いを示すかを指定しなければ問題が解けない。
このような条件を境界条件(boundary condition)という。
※媒質が無限に続く場合も，「無限の彼方では変位が0になる」という境界条件が考えられる。
以下では1次元の問題に限り，典型的な境界条件を示しておこう。
の領域の波動を考えるとき， での境界条件として最も簡単なものとして以下の２つがある。
では常に変位
が 0 になるよう固定されている場合を固定端の境界条件という。このときは，すべての時間
で，
が成り立つ。
波動方程式の一般解 
を使うと，
すなわち， 
となる。ここで，
はすべての値をとりうる変数とみなせるので，これを
と書いた。
したがって，
となる。
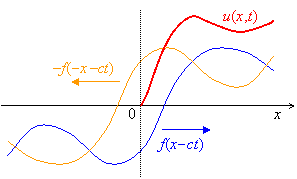
進行波
と 後退波
のグラフは，原点に関して回転対称であり，それらの合成により常に が保証される。
で常にひずみ 
が 0 になる場合を自由端の境界条件という。このときは，
が成り立つ。
このときは，
を使って，
すなわち，
となる。したがって，
となる。（補足説明）
定数
は 任意関数
に含めることができるので，
となる。
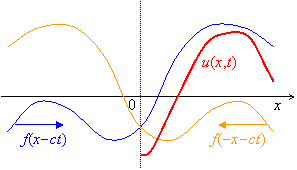
進行波
と 後退波
のグラフは，直線 に関して線対称であり，それらの合成により常に が成立する。
1次元の境界条件としては，上記の2つが最も簡単であるが，一般にはより複雑になる。
2次元・3次元の問題を解く場合も，同様に境界条件を与える必要がある。
境界での値が与えられているものをディリクレ(Dirichlet)の問題， 境界での微分係数が与えられているものをノイマン(Neumann)の問題という。固定端の境界条件はディリクレ問題の例，自由端の境界条件はノイマン問題の例である。
もちろん，これら以外の一般の境界条件もある。
2次元・3次元の問題では，境界の形状が特に簡単な場合を除いて解析的に解を求めることが難しいため，有限要素法などの数値解法が使われるのが普通である。
（補足説明） から を導くには次のように考えればよい。
の両辺をで積分したとき，
の左辺は
である。
右辺は，
とおくと，
であるから，
となる。したがって， となる。