弦の線密度が途中で変わる場合の横波

無限に長い弦であるが， と との部分で弦の線密度が変わる場合を考える。
張力は共通なので，これを とする。

の部分の線密度，波の速さ，変位をそれぞれ ，， とし，
同様に の部分の量には−の添え字を付けることにする。

なお，以下では とする。

境界条件は，
　　　　　，
　　　　　
である。

一般解
　　　　　
を代入すると，
　　　　　，
　　　　　
であるが， と置くと，

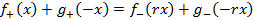
	(1)
	(2)

となる。
ここで， は，それぞれ， および で適用されるが，
は全領域で定義できることに注意しておこう。

具体例として， に向かって三角パルスが進む場合の反射を考える。

パルスの立ち上がりが に到達したときを とすると， は下図で与えられる。

このとき， に対しては であり， に対して 　である。
特に， としてよいので，境界条件は簡単になる。

まず， が，後退波 の最初の立ち上がりから頂点までの間にある場合を考える。
これは の時間に相当する。このとき，
　　　　　　　　　（ここで，　とした。）
であるから，これを(1)(2)に代入して，

	(3)
	(4)

を得る。(3)を で微分すると，
　　　　　
となる。(4)を使って を消去すると，
　　　　　
となるが， という初期条件を考慮すると，
　　　　　
が得られる。これと(3)から，
　　　　　
も得られる。

次に，三角波の後半部が境界を通過する場合を考える。
これは， の時間に相当し，このとき，境界付近では，
　　　　　
となる。これを(1)(2)に代入すると，

	(5)
	(6)

となる。先と同様に，初期条件 の下で解を求めると，
　　　　　，
　　　　　
が決まる。

最後に， の部分が境界に到達した以後，すなわち の場合を考えると，
(1)(2)より，
　　　　　
となる。

以上で，三角パルスの入射波 に対する，反射波 と透過波 が求められたことになる。

シミュレーションソフト　→　

問　以上の結果で， の場合は，反射は起こらず，そのまま透過することを確認せよ。
　　※ のとき，， になる。

問　の場合は，固定端における反射となることを確認せよ。
　　※ のとき，， となる。

問　 の場合は，自由端における反射となることを確認せよ。
　　※ のとき， になる。