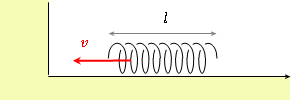
図のように自然長
，弾性定数
，質量
のばねが，自然長のまま一様な速さ
で，壁にぶつかる場合を考える。
これまで通り，ばねの内部の位置は
で表すことにし，ばねの一端（
）が壁に接したときを時刻
とする。このときの位置を基準に変位
を考える。
この後， は固定端となり，ばねの中で縦波が生じる。もちろん，
の端はずっと自由端のままである。
ばねの一端 が壁に接している間は，
初期条件 
， 
境界条件 
， 
のもとで波動方程式を解けばよい。
ばねが壁から離れるのは， の端のひずみが縮みから伸びに変わるとき，すなわち，
となるときである。
この後は，両端が自由端になり，このときの変位や各位置の速度を初期条件として波動方程式を解かなくてはならない。（しかし，後で見るように，この運動はごく簡単にわかる。）
では， が固定端となっているときのばねの運動を調べよう。
初期条件から，一般解は，
(1)
の形で，
である。ここで，
はばねの縦波の速さで，
である。
他の
に対する
の値は，境界条件から決める。
が固定端であることから，
，すなわち， は偶関数でなくてはならない。
一方， が自由端であることから，
，したがって，
であり， は点
に関して点対称となる。
これらより，定数を除いて は下図のような
周期の関数であることがわかる。
各点の速度は，
(2)
となり，
のグラフは下図のようになる。
各点の変位や速度は(1),(2)式と上記のグラフから容易に求めることができる。
変位 速度
これを言葉で説明すると次のようになる。
ばねは，壁側から縮んでゆき，縮んだ部分は静止する。
全体が一様に縮み，静止した後，自由端側からばねは速さ
全体が自然長に戻ったとき，ばねの各部分の速度は になっているので，ばねは自然長で元と逆向きに速さ で跳ね返っていく。
すなわち，ばねと壁は，弾性衝突をすることになる。
シミュレーションソフト → 
問 壁とばねの間に働く力を求めよ。また，壁とばねが接している時間を求め，その間にばねに加わる力積を求めよ。
（こたえ） 力 
， 時間 
， 力積 
