シュテファン=ボルツマンの法則 (Stefan-Boltzmann law)

絶対温度の黒体の単位表面積から 単位時間に放出される全放射エネルギーは，次のシュテファン=ボルツマンの法則で表される。
　　　　　
ここで，は シュテファン=ボルツマン定数と呼ばれる定数である。
　　　　　

熱放射がに比例することは， Stefan(1879)が実験的に示し，Boltzmann(1884)が理論的に説明した。

この法則は，Planckの公式を全振動数にわたって足し上げる（積分する）ことで得られ， これによりシュテファン=ボルツマン定数も， プランク定数などで表現できることになる。 （この計算は，こちらを参照）

黒体ではない場合は，物体が放射を吸収する割合（吸収率）を使って，
　　　　　
となる。（吸収率は振動数により異なるので，より正確な式はこのように簡単には書けない。）

例　惑星の表面温度

太陽定数，アルビド，温室効果

例　恒温動物

人間
カンガルーの赤ちゃん，胎生

Planckの公式からStefan=Boltzmannの法則を導出する

まず，温度の空間の単位体積当たりの放射エネルギー
　　　　　
と，温度の黒体の単位表面積に単位時間当たりに吸収される放射エネルギーの関係を考える。

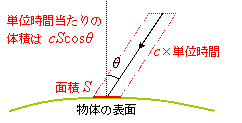
物体表面の微小な面積をとし， この面の法線からの角度で， 方位角で入射してくる放射エネルギーは， の体積中の放射エネルギーのうち， この方向を持つものの割合だけになる。（は光速度）

放射は等方的であるから，， の角度で入射するものの割合は，
　　　　　
となる。したがって，単位時間にこの角度から面積に入射する放射のエネルギーは，
　　　　　
になる。これをと で積分すれば，
　　　　　
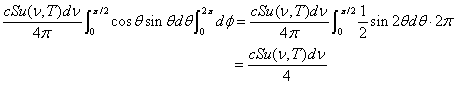
が得られる。したがって，単位時間，単位面積当たりに入射する放射エネルギーは， となる。 放射平衡の状態を考えているので，これが黒体の単位表面積から単位時間に放出される放射エネルギーでもある。

これをすべての振動数で積分すると，シュテファン=ボルツマンの法則が得られる。
とおくと，この積分は，
　　　　　
となる。ここで現れる定積分は である （証明はこちら）。したがって，
　　　　　　　　　　　　（Stefan=Boltzmannの法則）
となり，シュテファン=ボルツマン定数は，
　　　　　
で与えられることになる。

問　上式からシュテファン=ボルツマン定数の数値を計算せよ。

（こたえ）
　円周率　，
　ボルツマン定数　，
　光速度　，
　プランク定数　
などを代入して計算すると，となる。