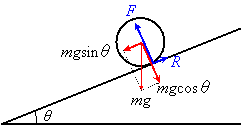

質量![]() の物体が受ける力は,
の物体が受ける力は,
重力![]() と 斜面からの抗力(垂直抗力
と 斜面からの抗力(垂直抗力![]() と摩擦力)
と摩擦力)
の2つであるが,それぞれを斜面に平行な向きと斜面に垂直な向きに分けて考える。
斜面に垂直な力は,重力の![]() と斜面から受ける垂直抗力
と斜面から受ける垂直抗力![]() であるが,物体が斜面に沿って運動するので,これらはつりあっている。
であるが,物体が斜面に沿って運動するので,これらはつりあっている。
斜面に平行な力は,重力の![]() と摩擦力
と摩擦力![]() であり,斜面下向きを正にとり,この向きの重心運動と,重心の周りの回転を考える。
であり,斜面下向きを正にとり,この向きの重心運動と,重心の周りの回転を考える。
物体の半径を![]() ,慣性モーメントを
,慣性モーメントを![]() ,回転角速度を
,回転角速度を![]() とすると,運動方程式は以下のようになる。
とすると,運動方程式は以下のようになる。
また,物体が斜面上を滑らずに転がるとすれば,
斜面下向きの重心の運動 (1) 重心の周りの回転 (2)
という関係が成り立つ。
したがって
(3)
(1)(3)より,![]() となり,さらに(2)を使って
となり,さらに(2)を使って![]() を消去すれば,
を消去すれば,
![]()
これより,角加速度![]() および加速度
および加速度![]() は,
は,
となり,いずれも一定になる。
,
(4)
等加速度運動であるから,初速度を![]() ,初期位置を
,初期位置を![]() とすれば,時刻
とすれば,時刻![]() の速度と位置は,
の速度と位置は,![]() ,
,![]() となる。
となる。
ちなみに摩擦力![]() は,(2)(4)より,
は,(2)(4)より,![]() となり,これも一定である。
となり,これも一定である。
さて,球・円柱・円管の慣性モーメント![]() は,それぞれ,
は,それぞれ,
球 ![]() , 円柱
, 円柱 ![]() , 球殻
, 球殻 ![]() , 円管
, 円管 ![]()
であるから,物体の加速度は,
球 ![]() , 円柱
, 円柱 ![]() , 球殻
, 球殻 ![]() , 円管
, 円管 ![]()
となり,この順に小さくなっていく。しかし,同じ形状であれば,半径や質量には依存しない。なお,![]() は,物体が回転せず,摩擦なしで滑り落ちるときの加速度である。
は,物体が回転せず,摩擦なしで滑り落ちるときの加速度である。
問 上記の物体と斜面の静止摩擦係数を![]() とするとき,物体が滑らずに転がることができる斜面の最大角を求めよ。また,この角度は,球,円柱,円管のいずれで最も大きくなるか。(どれが一番滑りにくいか。)
とするとき,物体が滑らずに転がることができる斜面の最大角を求めよ。また,この角度は,球,円柱,円管のいずれで最も大きくなるか。(どれが一番滑りにくいか。)
(こたえ) 物体と斜面間の垂直抗力は![]() であるから,静止摩擦力
であるから,静止摩擦力![]() は
は![]() を満たす。 これより,滑らずに転がるための条件は,
を満たす。 これより,滑らずに転がるための条件は,![]() となる。これより,静止摩擦係数が同じであるとすると,
となる。これより,静止摩擦係数が同じであるとすると,
・同じ形状であれば,滑らない斜面の最大角は,質量や慣性モーメントにはよらないこと,
・同じ半径であれば,慣性モーメントが小さい方が斜面の最大角は大きくなる(滑りにくい)こと
がわかる。
物体の高さが![]() だけ下がったときを考えると,その落下時間
だけ下がったときを考えると,その落下時間![]() は,
は,![]() で決まるので,
で決まるので,
重心の運動エネルギーの増加 ![]() ,
,
回転の運動エネルギーの増加 ![]()
となる。したがって,全運動エネルギーの増加は,
![]()
となり,重力がした仕事に等しい。
物体が滑らずに転がるときは,摩擦力はいつも静止した点に働くので仕事をしない。そのため,斜面を滑らずに転がる剛体については,力学的エネルギーが保存する。(ただし,このときの運動エネルギーには,回転の運動エネルギーも含めなくてはならない。)
※斜面が鉛直面内で曲線を描いているときも,斜面の微小部分を考え,上の![]() や
や![]() を微小量
を微小量![]() や
や![]() に置き換えると,
に置き換えると,
![]()
が示せるので,曲線状の斜面でも(滑らない場合は)力学的エネルギーが保存する。
※現実の物体では変形に伴い熱が発生し,その分は力学的なエネルギーが減少する。通常,この効果を「転がり摩擦」と称する。
逆に,物体が斜面上を滑りながら転がるときは,摩擦力が負の仕事をするので,力学的エネルギーは減少していく。
(参照)斜面の実験
(参考)固体と液体
ジュースの空き缶に水を入れて凍らせたものと,中が液体のままのジュースの缶を斜面で転がすと,どちらが速く転がるだろうか?
ジュースの缶の代わりに,ゆで卵と生卵を転がしてもよい。
内部が液体の場合は,固体とは異なり,内部が完全には回転しない。そのため,内部が液体である物体の慣性モーメントは,すべてが固体である場合に比べて小さくなる。慣性モーメント![]() が小さいと,斜面を下る加速度は大きくなる。
が小さいと,斜面を下る加速度は大きくなる。
液体が入った缶
Jackson K A et al, Viscous and non-viscous models of partially filled rolling
can, Am.J.Phys. 64, 277-82