このページの記号は,先のページと同じである。
まず,ばねの下端を力![]() で引き,静止させた場合の変位を求める。
で引き,静止させた場合の変位を求める。
つりあいの式,
![]() ,
, ![]()
と,境界条件
![]() ,
,
![]()
から,
![]()
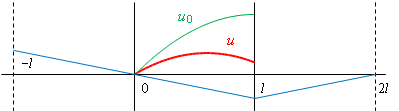
が得られる。ただし,![]() は,ばねが自重とつり合っている場合の変位で,
は,ばねが自重とつり合っている場合の変位で,
![]()
である。
力![]() により,ばねの下端はつり合いの位置から
により,ばねの下端はつり合いの位置から![]() 伸びるので,ばねの下端を
伸びるので,ばねの下端を![]() だけ引き下げた場合の変位は,
だけ引き下げた場合の変位は,
![]()
である。
これと初速度が0であることを初期条件とし,この状態で,手を離した後の運動を考える。
先のページで示したように,
![]()
とすると,![]() は通常の波動方程式を満たす。境界条件は,
は通常の波動方程式を満たす。境界条件は,
![]() ,
,
![]()
であり,初期条件は,
![]() ,
,
![]()
である。
解も先のページに示した手順に従えばよい。まず,
![]()
を,![]() に関して対称な,
に関して対称な,![]() 周期の奇関数に拡張して,
周期の奇関数に拡張して,
![]()
を得る。ここで,![]() は整数である。
は整数である。
この![]() を使って,求める変位は,
を使って,求める変位は,
![]()
で与えられる。
初期状態から半周期までを具体的に示しておく。
| (0) |
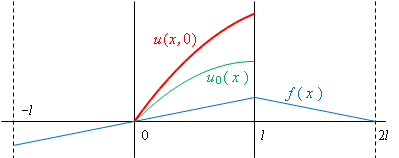 |
| (1) ばねは自由端から縮んでいく。 |
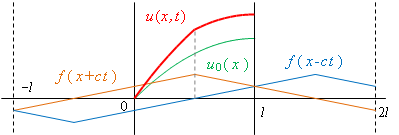 |
| (2) つりあいの状態を経過する。 |
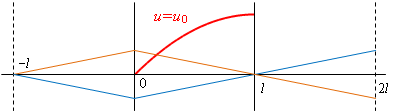 |
| (3) 固定端から縮んでいく。 |
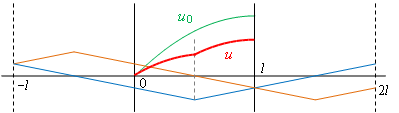 |
| (4) この後,ばねは逆の過程をたどり,初期状態に戻る。 |
 |