ここでは,ばねを鉛直にし,上端を固定端,下端を自由端にして振動させる場合を考える。ばね自身に加わる重力も考慮すると波動方程式自体も少し変わるが,結局は通常の波動方程式を解く問題に帰着することを示す。

弾性定数![]() ,線密度
,線密度![]() のばねを鉛直にぶらさげた場合を考える。また,ばねの各点を
のばねを鉛直にぶらさげた場合を考える。また,ばねの各点を![]() で表し,上端を
で表し,上端を![]() として,
として,![]() の増加方向を下向きにとる。
の増加方向を下向きにとる。
ばねの各点![]() の時刻
の時刻![]() における変位を
における変位を![]() とする。
とする。
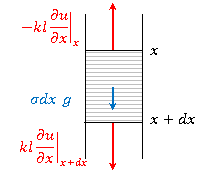
![]() と
と![]() の間の部分に働く力は,重力も加えて,
の間の部分に働く力は,重力も加えて,![]() となるので(詳細はこちらを参照),運動方程式は,
となるので(詳細はこちらを参照),運動方程式は,
(1)
となり,通常の波動方程式とは少し異なる。
ばねの上端は固定端,下端は自由端の場合を考える。ばねの自然長を![]() とすると,ばねの下端は
とすると,ばねの下端は![]() に対応する。
に対応する。
境界条件は,![]() は固定端,
は固定端,![]() は自由端であるから,
は自由端であるから,
,
(2) (3)
となる。
なお,![]() が自然長からのばね全体の伸びを表すことになる。
が自然長からのばね全体の伸びを表すことになる。
ばねの弾性力と重力がつり合って,ばねが静止しているときの変位![]() を求めるには,(1)で
を求めるには,(1)で ![]() として,
として,
![]() (ただし,
(ただし,![]() )
)
を解けばよい。さらに境界条件(2)(3)も使うと,
(4)
であることがわかる。ここで,![]() はばねの質量である。
はばねの質量である。
これから,ばねの自重による伸びは,
![]()
となることがわかる。また,各点のひずみは,
![]()
となる。この式は,ばねの上の方ほど伸び,下端では伸びが0になることを示しており,このことは直感的にもわかるだろう。
さて,つるしたばねの振動を考える際には,つりあいの位置からのずれを見る方が簡単である。そこで,
(5)
とすると,(1)は,
![]() ,
,
境界条件は,
![]() ,
,
![]()
となり,重力がない場合と全く同じ問題を解けばよいことになる。
例えば,初期条件として,変位の関数形![]() と初速度
と初速度![]() が与えられていると,
が与えられていると,
![]() (
( ![]() )
)
を元に,奇関数で,![]() に関して対称であり,
に関して対称であり,![]() 周期の関数を作れば,全領域での
周期の関数を作れば,全領域での![]() の関数形が決まる(先の例を参照)。
の関数形が決まる(先の例を参照)。
この![]() を使って,求める変位は,
を使って,求める変位は,
![]()
と書ける。
このことから,一般に,一端が固定端,他端が自由端であるばねの自重による振動の周期は,
![]()
であることもわかる。
具体例 1 ばねを自然長にして落下させた場合