弦を伝わる横波の速度

張力，線密度 の弦を伝わる横波の速度 は，

で与えられる。

これを導くには，弦の微小部分に対するニュートンの運動方程式から波動方程式を導き，波動方程式の係数から速度を求めるのが一般的な方法である。
しかし，ここではより簡単に横波の速度を求める方法を紹介しておく。

弦（ひも，ロープ，ばね）の横波が，下図のように右方向に進んでいるとする。このとき，変位の形は変化せずにそのまま右方向に速さ で進んでいく。（変位は周期的なものでなくてもよい。）

これを，波と同じ速さ で進む観測者から見ると，変位の形状は不動になるが，弦自身が左向きに動いていく。
これは，丁度，曲がったガラス管の中に紐を通して，その紐を引いたような感じになる。

※弦の変位が小さいという近似では，弦の各点の速さもであると考えてよい。

ガラス管が無くても，このような運動ができるための条件は以下のようになる。

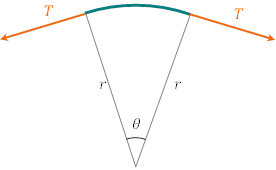
弦のごく小さな部分を取り出して考えると，半径 の円弧と考えることができる。このをその位置の曲率半径という。
すると，この部分は半径，速さ の円運動をすることになるので，この部分の質量を とすると，必要な向心力は， である。

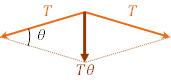
この向心力は，小さな円弧の両端に加わる張力 の合成により与えられなければいけない。円弧の中心角を とすると，この合力は，
　　　　　
となる。

弦の線密度（単位長さ当たりの質量）を とすると，微小な弦の質量は となる。したがって，
　　　　　
でなくてはならず，これより波の速さ は，
　　　　　
であることがわかる。