弦の横波 （波動方程式の導出）

張力が，線密度 の一様な弦を伝わる横波を考える。
※　線密度とは単位長さ当たりの質量のことで，単位は kg/m になる。

弦の微小部分に関するニュートンの運動方程式から波動方程式が導かれること，また弦を伝わる横波の速さが であることを示す。

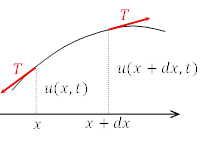
平衡の位置で静止している弦に沿って軸をとり，弦上の点 の時刻 における変位を とする。

位置 と の間にある長さ の微小部分に対する，軸に垂直な方向の運動方程式 を考える。

この部分の質量は であり，加速度は と書ける。

（補足） 弦の軸に垂直な方向の位置が であるから，その時間微分が速度，2階微分が加速度になる。

少し厄介なのが，力 である。この微小部分に働く力は，微小部分の両端に加わる張力の傾きがわずかに異なることから生じる。

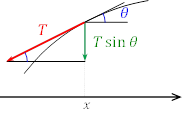
の位置での弦の傾角を とすると，微小部分の位置 に働く力の軸に垂直な成分は である。
弦の傾角 が弦上のどの場所でも小さいとすると，

　･･････・・・・・・・・・・・・・・ (1)

と近似できる。すると，位置に働く力は と書ける。

同様に，位置 に働く力は， となる。

これらを加えて，微小部分に働く力の軸に垂直な成分は，

と書けることになる。

ここで，微分法の定義式 を使うと，

となるから，力 は，

であることがわかる。

（参考）　ここで使った近似(1)の範囲では，力の方向の成分は0になる。

したがって，運動方程式 は，，すなわち，

　･･････・・・・・・・・・・・・・・・・・・・・・ (2)

という波動方程式の形になる。

波動方程式の一般形は，

であり， は波の速度を表す。（なぜ が波の速さになるのかは，波動方程式の一般解を参照のこと。）

したがって，弦を伝わる横波の速さは，

のように，張力と線密度で決まる。