ここでは，気体や液体中の縦波に対する運動方程式から波動方程式が得られることを示し，
さらに気体中の音速を表すLaplaceの式を導く。
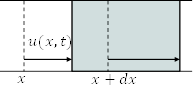
音波の進行方向に
軸をとり，時刻
における位置 の変位を 
とする。
軸に平行で断面積が
の気柱（液柱）を考え，その中の位置が と 
の間にある微小部分に対する運動方程式 
を作る。
気体（液体）の密度を
とすると，質量は 
である。
また，変位がこの微小部分の位置を表しているので，加速度は 
である。
この微小部分に加わる力
は，両側の面が受ける圧力の差から生じる。
圧力の変化は，体積の変化から生じる。圧力
が
増加すると，体積
が
減少する場合に，体積弾性率
を次式で定義する。
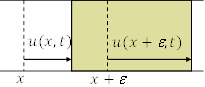
右図からわかるように，変位の勾配が体積の変化率になるので，位置 における圧力の増加は，
となる。同様に， における圧力の増加は次式になる。
と の間の微小部分が受ける力 は，両面から受ける圧力の差であるから，
と書ける。
したがって，運動方程式 は，
，
すなわち，
という波動方程式になる。
波動方程式の一般形 
と比較すると，音波の速度
は，
･･････････････････・・・・・・・・・・・・・・・・・ (1)
であることがわかる。
通常，音波の振動数は十分高いので，気体の圧縮・膨張は断熱変化と考えられる。
断熱変化の場合，圧力 と体積 には次の関係が成り立つ。
･･･････････････・・・・・・・・・・・・・・・ (2)
ここで，
は定圧比熱
と定積比熱
の比である。（比熱比 
）
(2)式を微分すると，
， すなわち， 
となるので，体積弾性率は，
となる。これを(1)に代入すると，気体中の音速は，
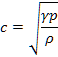
で与えられることがわかる。これをLaplaceの式ということがある。
問 断熱変化ではなく等温変化（
）だとすると，音速の式はどのようになるか。
（こたえ） 
となるので，
この音速の式に，実際の気体に応じて数値を入れれば，具体的な音速の値が求められる。