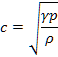 ・・・・・・・・・・・・・・・・・・・・・・・ (1)
・・・・・・・・・・・・・・・・・・・・・・・ (1)で与えられる。ここで,
空気中,水中,金属中の具体的な音速を理論式から計算してみよう。
それぞれの理論式の導出は,波動のページの「波動方程式の導出例」を参照のこと。
空気中の音速の理論式は,ラプラスの式
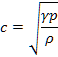 ・・・・・・・・・・・・・・・・・・・・・・・ (1)
・・・・・・・・・・・・・・・・・・・・・・・ (1)
で与えられる。ここで,![]() は比熱比,
は比熱比,![]() は気圧,
は気圧,![]() は空気の密度である。
は空気の密度である。
まず,0℃,1気圧の乾燥空気中の音速を計算する。
空気の比熱比 ![]() ,1気圧
,1気圧 ![]() ,密度
,密度 ![]() という値を(1)に代入すれば,
という値を(1)に代入すれば,
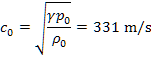
という値が得られる。
次に,気温の変化による音速の変化を考える。
このとき,気圧は1気圧のままで,比熱比![]() の温度変化は無視すると,音速の変化は,密度の変化だけから生じることになる。
の温度変化は無視すると,音速の変化は,密度の変化だけから生じることになる。
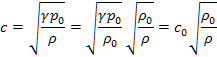
密度![]() は体積
は体積![]() に反比例し,等圧の理想気体とすれば,体積
に反比例し,等圧の理想気体とすれば,体積![]() は絶対温度
は絶対温度![]() に反比例するので,気温が
に反比例するので,気温が![]() ℃のときは,
℃のときは,
![]()
という関係が成り立つ。したがって,常温程度の気温に対しては,
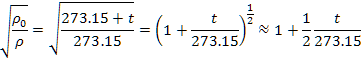
という近似式が使える。
これより,1気圧,![]() ℃の空気中の音速は,
℃の空気中の音速は,
![]()
という値になる。
これは実測値とよく一致し,気温が1℃上がると音速は 0.6 [m/s]速くなる。
特に,15℃のときの音速は,331+0.6×15 = 340 m/s となり,これが音速の値としてよく使われる。
水中の音速の理論式は,体積弾性率![]() を使うと,
を使うと,
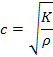 ・・・・・・・・・・・・・・・・・・・・・・・・・・・ (2)
・・・・・・・・・・・・・・・・・・・・・・・・・・・ (2)
と書ける。ここで,![]() は水の密度である。
は水の密度である。
体積弾性率の逆数を圧縮率といい,理科年表などでこの値を調べることができる。
水の圧縮率 ![]() から体積弾性率は
から体積弾性率は ![]() ,また密度は
,また密度は![]() であるので,水中の音速は,
であるので,水中の音速は,
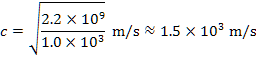
という値になる。これも実測値とよく一致する。
固体中の音速の理論式は,ヤング率![]() を使うと,
を使うと,
 ・・・・・・・・・・・・・・・・・・・・・・・・・・・ (3)
・・・・・・・・・・・・・・・・・・・・・・・・・・・ (3)
と書ける。ここで,![]() は固体の密度である。
は固体の密度である。
様々な金属のヤング率と密度は理科年表などで調べることができるので,音速も計算できる。
身近な金属中の音速は水中の音速より速い。
※金属棒で実験するときは,側面の影響も大きい。
| 金属 | 密度 g/cm3 | ヤング率 1010Pa | 音速 km/s |
|---|---|---|---|
| アルミニウム | 2.7 | 7.0 | 5.1 |
| 鉄 | 7.9 | 21 | 5.2 |
| 銅 | 9.0 | 13 | 3.8 |