ここでは,固体中の縦波に対する運動方程式から波動方程式が得られることを示し,さらに音速が密度とヤング率で表せることを示す。
※ここの説明は,気体中の音速の説明における 体積弾性率を ヤング率
で置き換えただけのものである。

音波の進行方向に![]() 軸をとり,
時刻
軸をとり,
時刻![]() における
位置
における
位置![]() の変位を
の変位を![]() とする。
とする。
![]() 軸に平行で
断面積が
軸に平行で
断面積が![]() の柱状の部分を考え, その中の位置が
の柱状の部分を考え, その中の位置が![]() と
と
![]() の間にある微小部分に対する 運動方程式を作る。
の間にある微小部分に対する 運動方程式を作る。
固体の密度を![]() とすると, 質量は
とすると, 質量は ![]() である。
である。
また,変位がこの微小部分の位置を表しているので, 加速度は ![]() である。
である。
この微小部分に加わる力は,両側の面が受ける力の差から生じる。その力は,フックの法則によりひずみに比例している。
 力とひずみの関係はヤング率で表せる。
断面積
力とひずみの関係はヤング率で表せる。
断面積![]() ,
長さ
,
長さ![]() の棒に 力
の棒に 力![]() を加えたときに, 棒が
を加えたときに, 棒が![]() 伸びた場合に, ヤング率
伸びた場合に, ヤング率
![]() を次式で定義する。
を次式で定義する。
![]()
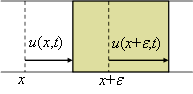
右図からわかるように,変位の勾配がひずみ![]() になるので,
位置
になるので,
位置![]() における力は,
における力は,
![]()
となる。同様に,![]() における力は 次式になる。
における力は 次式になる。
![]()
ここで,符号は![]() と
と ![]() の間の微小部分が受ける力となるように付けられている。
の間の微小部分が受ける力となるように付けられている。
結局,![]() と
と ![]() の間の微小部分が受ける力
の間の微小部分が受ける力 ![]() は,
は,
![]()
と書ける。
したがって,運動方程式 ![]() は,
は,
![]() ,
,
すなわち,
![]()
という波動方程式になる。
波動方程式の一般形 ![]() と比較すると,
音波の速度
と比較すると,
音波の速度![]() は,
は,
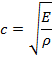
であることがわかる。
この音速の式に,実際の固体に応じて数値を入れれば,具体的な音速の値が求められる。
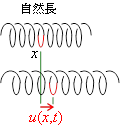
ばねを伝わる縦波の変位![]() も同様で,時刻
も同様で,時刻![]() に,自然長のときに位置
に,自然長のときに位置![]() にあった部分が
にあった部分が![]() 方向に
方向に![]() だけ移動していることを表す。
だけ移動していることを表す。
ただし,ばねの断面積![]() には物性的な意味が無いためヤング率が定義できない。そこで,お馴染みのばねの弾性定数
には物性的な意味が無いためヤング率が定義できない。そこで,お馴染みのばねの弾性定数![]() を使うことにする。また,密度
を使うことにする。また,密度![]() の代わりに 線密度
の代わりに 線密度![]() を使うのが自然である。これらを使って波動方程式を書くことにする。
を使うのが自然である。これらを使って波動方程式を書くことにする。
自然長![]() のばねに張力
のばねに張力![]() を加えたときの伸びを
を加えたときの伸びを![]() とすると,ばねの弾性定数
とすると,ばねの弾性定数![]() は,
は,
![]()
で定義される。
したがって,ひずみ![]() に対する力は
に対する力は![]() であり,
であり,![]() と
と![]() の間の部分に働く力は
の間の部分に働く力は ![]() となる。
となる。
また,その部分の質量は![]() であるから,運動方程式
であるから,運動方程式
![]()
から波動方程式
![]()
が得られる。ここで![]() は,ばねの縦波の速さで,
は,ばねの縦波の速さで,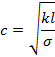 で与えられる。
で与えられる。
次に,このばねを長さ![]() に引き延ばした場合の波の速さを考えよう。
に引き延ばした場合の波の速さを考えよう。
長さ![]() に引き延ばすと,張力は
に引き延ばすと,張力は ![]() となる。
となる。
この状態から,さらにばねを![]() だけ伸ばすと,張力は,
だけ伸ばすと,張力は, ![]() になる。
になる。
すなわち,ひずみ×![]() だけ力が変化する。
だけ力が変化する。
長さ![]() になったばねに改めて
になったばねに改めて![]() 座標値を割り付け,その
座標値を割り付け,その![]() の部分を考える。この部分が受ける力は,
の部分を考える。この部分が受ける力は,
![]()
である。ばねの質量を![]() とすると,線密度は
とすると,線密度は![]() となり,微小部分の質量は
となり,微小部分の質量は![]() である。
である。
すると,波動方程式,
![]()
が得られる。縦波の速さは,
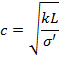
となり,自然長の場合と同じ形になる。
これに,![]() を代入すると,
を代入すると,
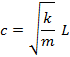
となり,波の速さはばねの全長![]() に比例する。
に比例する。
その結果,ばねを任意の長さに伸ばしても,このばねを縦波が一往復する時間![]() は同じで,
は同じで,
![]()
となる。
このことは,ばねの部分ごとに伸びが違っても成り立つので,スリンキーのようなばねを両端で固定し,ぶら下げて実験することができる。
(注) これは,ばねを伝わる縦波の実験をした場合に言えることである。
ばねを伝わる横波の場合は,弦の振動と同様に波の速さは![]() となり,この場合の往復時間は一定にはならない。
となり,この場合の往復時間は一定にはならない。