ばねに働く重力も考慮した波動方程式は，
であり，境界条件は，両端ともに自由端であるから，
である。
初期条件は，
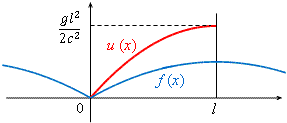
である。ここで，
は上端
が固定され，自重で伸びて静止しているばねの変位である。
とおけば，(1)は通常の波動方程式になり，境界条件，初期条件は上と同じ形，
， 
，
になる。
この場合の解は，
を元に，
周期の偶関数を作り，それを使って，
で与えられる。
本来の変位で書きなおすと，
となる。
運動の様子を具体的に追跡すると以下のようになる。
(0) 
のとき
(1) 
のとき
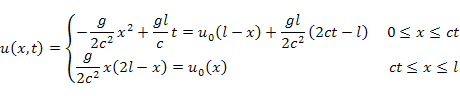
ばねの下部は，重力とばねの張力がつり合ったままであるから静止したままである。
ばねの上部から落下が始まるが，その上端の落下速度は一定値である。
(2) 
のとき
(3) 
のとき
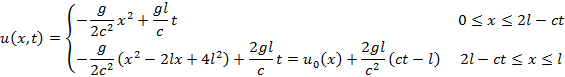
上端からの波動が下端に到達すると，下端も落下を始める。
上部は先ほどまでと同じ一定の速度で落下を続ける。
下部の落下速度も一定値であるが，上部の２倍の速度で落下する。
以下同様に，上部，下部共に一定速度で落下し，その速度は１周期ごとに増加していく。ただし，上部と下部では速度変化の時期が半周期ずれている。
ばねの下端と上端の位置をグラフにすると下図のようになる。
ばねの下端と上端は不思議な動きをするが，ばね全体の重心は，一定加速度
の自由落下運動をしているはずである。
問 重心の運動がどうなるか，実際に計算してみなさい。 ヒント
この運動を実際に観察するには，よく伸びてかつ自然長から十分に縮むことができるようなばねが必要になる。このようなばねは，なかなか無いだろう。
"スリンキー"は，自然長の状態で隙間が無い状態のばねであるので，縮むことができない。
先の変位のグラフで，変位の傾きが負になっているところはばねが縮んでいるところである。
最初の段階から，ばねが自然長より縮む部分が現れるので，理論とはかなり違ってくるはずである。
しかし，実際には，上図の
のあたりまで，理論にかなり近い動きが観察できる。
