の立方体の容器に，質量
の点状の分子が
個閉じ込められているとする。はアボガドロ数程度のきわめて大きな数である。一辺の長さが の立方体の容器に，質量 の点状の分子が 個閉じ込められているとする。はアボガドロ数程度のきわめて大きな数である。
地上では分子は放物運動をするが，分子の速度は十分に速く，かなり頻繁に壁や他の分子に衝突するので，衝突から次の衝突までの分子の軌跡は直線と考え，重力は無視する。
また，分子の速度分布は等方的で，あらゆる方向に均等に運動しており，どの方向をとっても粒子の速さの分布は等しい。ここでは，簡単化のために，すべての分子が平均の速さ
で動いており，その方向は，左右上下前後の6つの方向に限られているとする近似で考える。
まず，右側の壁面に衝突する分子を考え，これから圧力を求めよう。
運動量
の分子が壁に垂直に弾性衝突をして，同じ大きさ運動量で逆向きに跳ね返されると，この分子や壁に加わった力積の大きさは
である。
単位時間に衝突する分子数は，
の体積中の右向きの分子数であるから，
である。
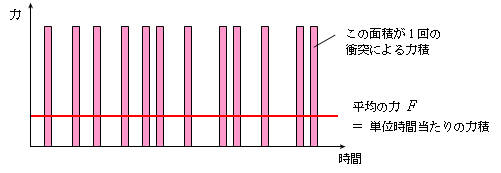
単位時間当たりの力積が，壁が受ける平均の力
であるから，
となる。したがって，壁に加わる圧力
は，
(1)
となる。ここで，
は気体の体積である。
上式より，
が得られるが，これを
モルに対する理想気体の状態方程式
と比較し，
（
はアボガドロ数）であることを使うと，
(2)
であることがわかる。最後に登場した
は，ボルツマン定数と呼ばれる。
気体定数は1モル当たりの量であるが，
は1分子当たりの気体定数という意味になる。
つまり，1分子に対する状態方程式は，となる。
この関係式は，理想気体の1分子の平均運動エネルギー
が，
となることを表している。したがって，気体全体が持っている内部エネルギー
は，
(3)
となる。一定量の気体に対しては，内部エネルギーは温度
のみで決まることもわかる。
上記のことから，逆に，理想気体とは気体分子が構造を持たない質点であると近似した場合に相当することがわかる。
現実の気体分子は，大きさを持っており，分子間力も働くので，質点とは異なるため理想気体ではない。しかし，単原子分子の気体である不活性ガス（He, Ne など）は理想気体に近い。
上記の式で，現れる 3 という係数は，空間が3次元であることに由来する。
点状の分子は，3次元空間内で3つの方向に運動することができるので，自由度3を持つといわれる。
1分子の平均運動エネルギーは，上述のようにであるが，このことを，
1自由度当たりの平均エネルギーは，
ということもできる。こちらは，より一般に，位置エネルギーを含む場合にも成り立つ表現である。
（参考１） ここで示した近似では，1分子の平均の運動エネルギーが，
のように平均の速さ の2乗で表されているが，より現実的に速さに分布を入れて計算すれば，
の平均値
となることがわかる。
速さに分布を入れた場合の計算例 任意の方向を考慮した一般的な計算例
（参考２） 式(1)より，
となることがわかるが，これは，理想気体の圧力がエネルギー密度
の2/3倍になることを示している。一般に，圧力とエネルギー密度の関係式を状態方程式ということもある。