は，波動方程式ここでは，両端が固定された一様な弦の振動を考える。
弦の変位 は，波動方程式
を満たす。ここで，
(1)
は弦を伝わる横波の速さで，
弦の張力を
，弦の線密度
とすると，
で与えられる。 （導出はこちら）
波動方程式(1)の一般解は，進行波と後退波の重ね合わせであり，
と書ける。（導出はこちら）
(2)
境界条件として
と 
が固定端であるとする。
したがって，
である。
まず，
より，
であるから，
(2)は，
となる。
(3)
次に，
において，
と書くと，
となるから，
は 
周期の関数であることになる。
初期条件として，
初期変位 
，
初期速度 
の場合を考える。
まず，前者からは，
が得られる。
(4)
また，速度は 
であるから，後者より 
，
したがって，
となる。
ここで，(3)をみると，定数
は0としても一般性を失わないことがわかる。したがって，
としてよい。すなわち
は奇関数である。すると(4)より，
となる。
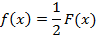
(5)
は，区間 
でしか与えられていないが，
は 周期の奇関数であるので，
これで完全に が決まる。
また が奇関数であることから，(3)は，
と書くことができる。これに，上記のように決めた
(6)
を使えば，境界条件と初期条件を満たす解の具体形が得られる。
（注）
と書けることになる。
さらに具体的に，初期の弦の形 が下図の赤で示したものである場合を考えよう。
これは，弦のある位置を引っ張り，そこで離して振動を開始させることになるので，ギターの弦を弾く場合に対応している。
は，区間 では
の半分に等しく， 周期の奇関数であることから，
上図の青で示したグラフになる。
(6)は，進行波，後退波ともに同じ のグラフを速さ
で平行移動したものになることを示しているので，それらを描き，合成すれば，下図のように弦の振動の具体形が得られる。
ギター弦の振動 
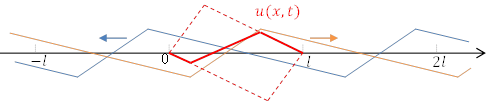
（参考）ギター弦は実際このような形で振動している。この形は，基本振動，2倍振動，3倍振動，・・の特定の重ね合わせになっている。
摩擦があるので振動は減衰していくが，その際に高い倍音の方が減衰が速いので，撥弦後しばらくすると基本振動に近い形になる。
（補足）上記では，すべて数式によって解を求めたが，少し慣れると，以下のように図形的に考えることができるようになる。
まず，初速度0であるから，進行波と後退波の形は同じで，時刻
には完全に重なっており，弦が存在する部分では初期変位の半分になる。
固定端では，進行波と後退波は回転対称になる。弦の両端で常に回転対称になることを考えると，上記のになることがわかる。
