が各時刻
にどのような変位をしているかを指定しなくてはならず，
という変位を表す関数を与えることになる。波または波動とは，空間の各点における何らかの振動が，隣の点にも影響を与えて，各点の振動状態が時間とともに空間的に伝わっていく現象をいう。
波動を表すには，空間の各点 が各時刻 にどのような変位をしているかを指定しなくてはならず， という変位を表す関数を与えることになる。
以下では，簡単な1次元の波動のみを考える。
このとき，波が伝わる方向を
方向とすると，変位は
で表せる。
それでも，変位はベクトルであるから，変位の向きは方向とは限らない。
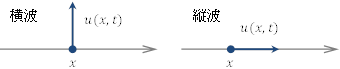
特に，変位の方向が，波の進行方向と平行なものを縦波（粗密波），波の進行方向と垂直なものを横波という。
一般の波は，縦波でも横波でもなく，両方の成分を持っている。
シミュレーション 横波・縦波・トロコイド波 縦波のグラフ表示
縦波の典型的な例は空気中の音波であり，その他液体中や固体中でも縦波(音波)が生じる。地震のP波も縦波である。
横波の例としては，弦の振動や電磁波が挙げられる。
水面に生じる波は，縦波・横波両方の成分を持っている。
（注）電磁波では，振動しているものは媒質ではなく電界や磁界なので，上記の「変位」という言葉は適切ではない。
しかし，電界や磁界が変化する向きは電磁波の進行方向に対して垂直なので横波になる。
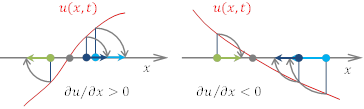
横波の変位のグラフは，そのまま弦などの媒体の形を表しているので，わかりやすいが，縦波の変位のグラフと実際の変位の様子は直感的な関係ではないので，理解するには少し慣れが必要である。
右図のように，
のところは媒質が伸びており，
逆に，
の部分では，媒質が縮んでいる。
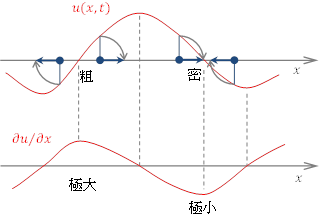
最も伸びている部分を「粗」の位置といい，これは変位の勾配が正で最も大きいところ，すなわち 
の極大の位置に対応する。
一方，最も縮んでいる部分を「密」の位置という。こちらは，変位の勾配が負で最も小さいところ，すなわち の極小の位置に対応する。
※右図では，粗や密の位置が変位が0となる位置のように描かれているが，必ずしもそうとは限らない。
変位が正弦関数で与えられる波動を正弦波という。ここでは，1次元の正弦波のみを考える。
振幅
，波長
，周期
で，方向に進む正弦波の変位は以下のように書ける。
･･･・・・・・・・・・・・・・・・ (1)
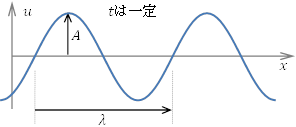
波長は，右図のように，時間を固定して変位をみたときの1周期分の長さである。
波長は，長さであるから，単位は m になる。
位置 が波長 だけ変化すると，位相（角度）は1周期分つまり
変わるので，
関数の中で は，
という形で現れる。
という形がよく出てくるので，これを
と書くことが多い。
この は，波数（または伝播数）と呼ばれます。
※元来，「波数」は波長の逆数
を表す言葉である。
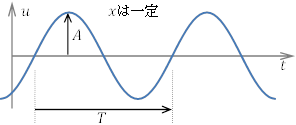
周期 は，右図のように，位置 を固定して（1つの場所で）変位をみたときの1周期分の時間である。
周期は，時間であるから，単位は s になる。
時間 が周期 だけ変化すると，位相は 変わるので， 関数の中で は，
という形で現れる。
振動数
は，1秒間に何周期の振動が起こるかを表す量で，周期 の逆数になる。
， 
振動数の 倍という形がよく出てくるので，これを角振動数
という。
振動数や角振動数の単位は，1/s であるが，これを Hz （ヘルツ）ともいう。
これらの量を使うと，正弦波の変位(1)は，次のようにも書き直せる。
の項と の項が逆符号で入っているのは， の正の向きに進む波を表しているためである。これを進行波という。
の負の向きに進む波（後退波）であれば，
になる。
波の速さ
は，波長と振動数の積になる。
1回の振動で波は だけ進むから，1秒間に 回の振動があれば，波は
進むことになり，上の関係が得られる。
波の速さ を使うと，変位の式は，さらにさまざまな形で表現できる。
たとえば，
より 
と書けるので，
進行波 
，
後退波 
と表すこともができる。
この形にすると，それぞれが進行波，後退波であり，波の速度がであることがわかる。
※ 波動方程式の一般解 も参照のこと。
中心から球面上に広がっていく波の振幅は，中心からの距離
に反比例し，
の形になる。したがって，球状に広がっていく正弦波の変位は次のように書ける。
