

電気力線は向きを持った曲線で,その曲線上の各点における接線の向きが
電界![]() の向きと一致するものである。
の向きと一致するものである。
電気力線は正の電荷から出て,負の電荷には吸い込まれることになる。
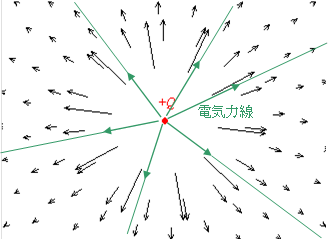
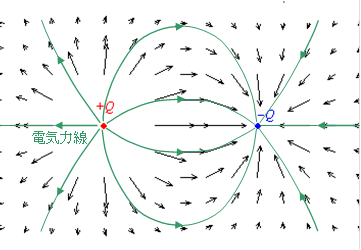
クーロンの法則から,点状の電荷![]() が作る電界の大きさは
が作る電界の大きさは![]() であり,電荷からの距離
であり,電荷からの距離![]() の2乗に反比例する。
の2乗に反比例する。
一方,電気力線は電荷![]() から四方八方に広がるので,ある電気力線の束が貫く面積は,距離
から四方八方に広がるので,ある電気力線の束が貫く面積は,距離![]() の2乗に比例する。 つまり,単位面積当たりの電気力線の数は,距離
の2乗に比例する。 つまり,単位面積当たりの電気力線の数は,距離![]() の2乗に反比例する。
の2乗に反比例する。

このため, 電界の強さは,単位面積当たりの電気力線の本数(電気力線の密度)と比例すると考えてよい。
このとき,電気力線の数は途中で増えたり,減ったりしないとしなければならない。
そこで,電気力線の「本数」を定量的に扱えるよう,次のように定義してみる。
電界の強さは,その位置の単位面積を垂直に通過する電気力線の「本数」に等しい。
そうすると点電荷![]() から距離
から距離 ![]() の位置では, 単位面積あたり
の位置では, 単位面積あたり ![]() 本の電気力線があることになる。 半径
本の電気力線があることになる。 半径![]() の球面全体を貫く電気力線の総数は, これに球の表面積
の球面全体を貫く電気力線の総数は, これに球の表面積 ![]() を掛けて
を掛けて ![]() 本になる。
本になる。
すなわち,電荷![]() からは,
からは, ![]() 本の電気力線が出ると考えればよいことになる。
本の電気力線が出ると考えればよいことになる。
このような議論ができるのは,クーロンの法則が ![]() の形をしているおかげである。
の形をしているおかげである。
※もちろん,電気力線の「本数」は,実際には数えられるものではない。
![]() の単位が
の単位が ![]() であることからも普通の本数(無次元)ではないことがわかる。
であることからも普通の本数(無次元)ではないことがわかる。
電界の大きさ×面積 のことを,より直感的にわかりやすい電気力線の本数という言葉で表現しているだけである。
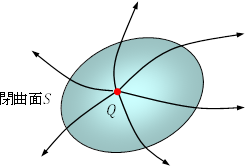
上記のことから,ある閉曲面![]() 上の各点での電界がわかれば, その閉曲面を貫く電気力線の総「本数」がわかり,したがって,その閉曲面の内部にある電荷量がわかる。
上の各点での電界がわかれば, その閉曲面を貫く電気力線の総「本数」がわかり,したがって,その閉曲面の内部にある電荷量がわかる。
これを式で書くと,次のガウスの定理になる。
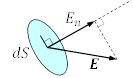
ここで,![]() は, 電界
は, 電界![]() の面
の面 ![]() に垂直で外向きの成分を表す。 また,
に垂直で外向きの成分を表す。 また,![]() は閉曲面の内部にある全電荷である。
は閉曲面の内部にある全電荷である。
対称性をもった電荷の分布が与えられおり,その周囲の電界の向きが正確にわかる場合には, ガウスの定理を使って電界の強さを求めることができる。